
分析 根据条件进行归纳得到x0满足xk-1=3xk-2-2=3k-1x0-2×3k-2≤244,xk=3xk-1-2=3kx0-2×3k-1>244,解不等式组,令k=8即可得到答案.
解答 解:x1=3x0-2
x2=3x1-2=32x0-2×3-2
x3=3x2-2=33x0-2×32-2×3-2
…
xk=3xk-1-2=3kx0-2×3k-1…-2×3-2
=3kx0-2×(3k-1 +…+3+1)
=3kx0-3k+1
若赋值k次后该过程停止,则x0的满足
xk-1=3xk-2-2=3k-1x0-3k-1+1≤244
xk=3xk-1-2=3kx0-3k+1>244
解得x0∈(35-k+1,36-k+1],(k∈N*).
则当k=8时,x0∈(35-8+1,36-8+1],
即$\frac{28}{27}<{x_0}≤\frac{10}{9}$,
故答案为:$\frac{28}{27}<{x_0}≤\frac{10}{9}$
点评 本题主要考查归纳推理的应用,其中根据已知条件中的定义,得到x0的满足的不等式组,是解答本题的关键.考查学生的运算和推理能力.


 53随堂测系列答案
53随堂测系列答案科目:高中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
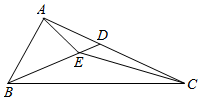 已知△ABC,点E是三角形内一点,BE延长后交AC于点D,设∠DBC=30°,∠DCE=10°,∠ECB=20°,∠DBA=40°.
已知△ABC,点E是三角形内一点,BE延长后交AC于点D,设∠DBC=30°,∠DCE=10°,∠ECB=20°,∠DBA=40°.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{16}$ | B. | $\frac{9}{16}$ | C. | $\frac{3}{8}$ | D. | $\frac{5}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com