
分析 (1)(法一)根据向量的运算法则计算出|$\overrightarrow{{{P}_{1}P}_{2}}$|=|$\overrightarrow{{{P}_{1}P}_{3}}$|=|$\overrightarrow{{{P}_{2}P}_{3}}$|,从而判断三角形的形状;
(法二)设出坐标,根据坐标运算得到P1P2=P1P3=P2P3,判断三角形的形状;
(2)根据向量乘积是0,得到向量垂直即可.
解答 证明:(1)(法一)∵$\overrightarrow{O{P}_{1}}$+$\overrightarrow{O{P}_{2}}$+$\overrightarrow{O{P}_{3}}$=$\overrightarrow{0}$,
∴$\overrightarrow{O{P}_{1}}$+$\overrightarrow{O{P}_{2}}$=-$\overrightarrow{O{P}_{3}}$,
∴${(\overrightarrow{{OP}_{1}}+\overrightarrow{{OP}_{2}})}^{2}$=${\overrightarrow{{OP}_{3}}}^{2}$,
∴${\overrightarrow{{OP}_{1}}}^{2}$+2$\overrightarrow{{OP}_{1}}$•$\overrightarrow{{OP}_{2}}$+${\overrightarrow{{OP}_{2}}}^{2}$=${\overrightarrow{{OP}_{3}}}^{2}$,
∵|$\overrightarrow{O{P}_{1}}$|=|$\overrightarrow{O{P}_{2}}$|=|$\overrightarrow{O{P}_{3}}$|=1,∴${\overrightarrow{{OP}_{1}}}^{2}$=${\overrightarrow{{OP}_{2}}}^{2}$=${\overrightarrow{{OP}_{3}}}^{2}$=1,
∴$\overrightarrow{{OP}_{1}}$•$\overrightarrow{{OP}_{2}}$=-$\frac{1}{2}$,
${|\overrightarrow{{{P}_{1}P}_{2}}|}^{2}$=|$\overrightarrow{{OP}_{2}}$-$\overrightarrow{{OP}_{1}}$|2=${\overrightarrow{{OP}_{2}}}^{2}$-2$\overrightarrow{{OP}_{1}}$•$\overrightarrow{{OP}_{2}}$+${\overrightarrow{{OP}_{1}}}^{2}$=3,
∴|$\overrightarrow{{{P}_{1}P}_{2}}$|=$\sqrt{3}$,同理|$\overrightarrow{{{P}_{1}P}_{3}}$|=|$\overrightarrow{{{P}_{2}P}_{3}}$|=$\sqrt{3}$,
∴△P1P2P3是正三角形;
(方法二)设P1(x1,y1),P2(x2,y2),P3(x3,y3),
∵|$\overrightarrow{{OP}_{1}}$|=|$\overrightarrow{{OP}_{2}}$|=|$\overrightarrow{{OP}_{3}}$|=1,∴$\left\{\begin{array}{l}{{{x}_{1}}^{2}{{+y}_{1}}^{2}=1}\\{{{x}_{2}}^{2}{{+y}_{2}}^{2}=1}\\{{{x}_{3}}^{2}{{+y}_{3}}^{2}=1}\end{array}\right.$,
∵$\overrightarrow{O{P}_{1}}$+$\overrightarrow{O{P}_{2}}$+$\overrightarrow{O{P}_{3}}$=$\overrightarrow{0}$,
∴$\left\{\begin{array}{l}{{x}_{1}{+x}_{2}{+x}_{3}=0}\\{{y}_{1}{+y}_{2}{+y}_{3}=0}\end{array}\right.$,
∴$\left\{\begin{array}{l}{{x}_{1}{+x}_{2}={-x}_{3}}\\{{y}_{1}{+y}_{2}={-y}_{3}}\end{array}\right.$,
∴${{(x}_{1}{+x}_{2})}^{2}$+${{(y}_{1}{+y}_{2})}^{2}$=${{x}_{3}}^{2}$+${{y}_{3}}^{2}$,
∴2x1 x2+2y1 y2=-1,
∴p1p2=$\sqrt{{{(x}_{1}{-x}_{2})}^{2}{+{(y}_{1}{-y}_{2})}^{2}}$=$\sqrt{3}$,
P1P3=P2P3=$\sqrt{3}$,∴P1P2=P1P3=P2P3,
∴△P1P2P3是正三角形;
(2)OP1⊥P2P3,
证明:∵$\overrightarrow{O{P}_{1}}$+$\overrightarrow{O{P}_{2}}$+$\overrightarrow{O{P}_{3}}$=$\overrightarrow{0}$,∴$\overrightarrow{O{P}_{1}}$=-$\overrightarrow{O{P}_{2}}$-$\overrightarrow{O{P}_{3}}$,
∴$\overrightarrow{{OP}_{1}}$•$\overrightarrow{{{P}_{2}P}_{3}}$=$\overrightarrow{{OP}_{1}}$($\overrightarrow{{OP}_{3}}$-$\overrightarrow{{OP}_{2}}$)
=(-$\overrightarrow{{OP}_{2}}$-$\overrightarrow{{OP}_{3}}$)($\overrightarrow{{OP}_{3}}$-$\overrightarrow{{OP}_{2}}$)
=${\overrightarrow{{OP}_{2}}}^{2}$-${\overrightarrow{{OP}_{3}}}^{2}$,
∵|$\overrightarrow{O{P}_{1}}$|=|$\overrightarrow{O{P}_{2}}$|=|$\overrightarrow{O{P}_{3}}$|=1,${\overrightarrow{{OP}_{2}}}^{2}$=${\overrightarrow{{OP}_{3}}}^{2}$,
∴$\overrightarrow{{OP}_{1}}$•$\overrightarrow{{{P}_{2}P}_{3}}$=0,OP1⊥P2P3.
点评 本题考查了向量的运算,向量垂直问题,考查向量的模以及两点间的距离,是一道中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{2}$ | B. | -$\frac{3}{2}$ | C. | 3 | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
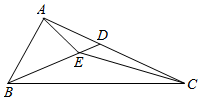 已知△ABC,点E是三角形内一点,BE延长后交AC于点D,设∠DBC=30°,∠DCE=10°,∠ECB=20°,∠DBA=40°.
已知△ABC,点E是三角形内一点,BE延长后交AC于点D,设∠DBC=30°,∠DCE=10°,∠ECB=20°,∠DBA=40°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com