
分析 (1)利用两角差的正弦、余弦公式把条件展开,解方程求得$\frac{tanα}{tanβ}$的值.
(2)利用同角三角函数的基本关系求得cos(α+β)和cos(α-β)的值,再利用两角差的正弦、余弦公式求得cos2α,sin2α的值.
解答 解:(1)∵sin(α+β)=sinαcosβ+cosαsinβ=$\frac{4}{5}$,sin(α-β)=sinαcosβ-cosαsinβ=-$\frac{12}{13}$,
∴sinαcosβ=-$\frac{4}{65}$,cosαsinβ=$\frac{56}{65}$,∴$\frac{tanα}{tanβ}$=$\frac{sinαcosβ}{cosαsinβ}$=-$\frac{1}{14}$.
(2)若$\frac{π}{2}$<α+β<π,-$\frac{π}{2}$<α-β<$\frac{π}{2}$,则cos(α+β)=-$\sqrt{{1-sin(α+β)}^{2}}$=-$\frac{3}{5}$,cos(α-β)=$\sqrt{{1-sin}^{2}(α-β)}$=$\frac{5}{13}$,
∴cos2α=cos[(α+β)+(α-β)]=cos(α+β)cos(α-β)-sin(α+β)sin(α-β)=-$\frac{3}{5}$•$\frac{5}{13}$-$\frac{4}{5}$•(-$\frac{12}{13}$)=$\frac{33}{65}$,
sin2α=sin[(α+β)+(α-β)]=sin(α+β)cos(α-β)+cos(α+β)sin(α-β)=$\frac{4}{5}•\frac{5}{13}$+(-$\frac{3}{5}$)•(-$\frac{12}{13}$)=$\frac{56}{65}$.
点评 本题主要考查同角三角函数的基本关系,两角差的正弦、余弦公式的应用,属于基础题.


 名题金卷系列答案
名题金卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
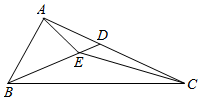 已知△ABC,点E是三角形内一点,BE延长后交AC于点D,设∠DBC=30°,∠DCE=10°,∠ECB=20°,∠DBA=40°.
已知△ABC,点E是三角形内一点,BE延长后交AC于点D,设∠DBC=30°,∠DCE=10°,∠ECB=20°,∠DBA=40°.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{16}$ | B. | $\frac{9}{16}$ | C. | $\frac{3}{8}$ | D. | $\frac{5}{8}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com