
分析 利用对数函数的性质求函数的定义域和值域,注意分母应不为0.
解答 解:∵函数为y=$\frac{1}{l{og}_{2}(x-2)}$,要使函数有意义,
∴x-2>0且x-2≠1,
∴函数的定义域为(2,3)∪(3,+∞).
∵log${\;}_{2}^{x-2}$的值域为R,但是log${\;}_{2}^{x-2}$在分母上,
∴log${\;}_{2}^{x-2}$的值域为(-∞,0)∪(0,+∞),
∴函数y=$\frac{1}{l{og}_{2}(x-2)}$的定义域为(-∞,0)∪(0,+∞),
故答案为:(2,3)∪(3,+∞);(-∞,0)∪(0,+∞).
点评 本题考查了与对数函数有关的复合函数的定义域以及值域的求法,要求熟练掌握复合函数的定义域与值域求法,考查学生的计算能力,属于中档题.


 口算题天天练系列答案
口算题天天练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-$\frac{{\sqrt{3}}}{3}$,$\frac{{\sqrt{3}}}{3}}$] | B. | (-∞,-$\frac{{\sqrt{3}}}{3}$]∪[$\frac{{\sqrt{3}}}{3}$,+∞) | C. | [-$\sqrt{3}$,$\sqrt{3}}$] | D. | (-∞,-$\sqrt{3}$]∪[$\sqrt{3}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
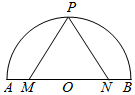 如图,AB是半圆O的直径,P是半圆$\widehat{AB}$上的任意一点,M、N是AB上关于O点对称的两点,若|AB|=6,|MN|=4,则$\overrightarrow{PM}$•$\overrightarrow{PN}$=( )
如图,AB是半圆O的直径,P是半圆$\widehat{AB}$上的任意一点,M、N是AB上关于O点对称的两点,若|AB|=6,|MN|=4,则$\overrightarrow{PM}$•$\overrightarrow{PN}$=( )| A. | 3 | B. | 5 | C. | 7 | D. | 13 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 身高(单位:cm) | [180,185) | [185,190) | [190,195) | [195,200) | [200,205) | [205,210] |
| 人数 | 2 | 3 | 3 | 2 | 1 | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\frac{3}{2}$ | C. | $\sqrt{3}$ | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com