
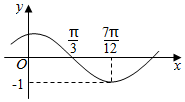
 函数f(x)=Asin(ωx+φ)(A>0,|φ|<$\frac{π}{2}$)的图象如图所示,为了得到g(x)=sin(2x+$\frac{π}{2}$)的图象,则只需将f(x)的图象( )
函数f(x)=Asin(ωx+φ)(A>0,|φ|<$\frac{π}{2}$)的图象如图所示,为了得到g(x)=sin(2x+$\frac{π}{2}$)的图象,则只需将f(x)的图象( )| A. | 向右平移$\frac{π}{6}$个单位长度 | B. | 向右平移$\frac{π}{12}$个单位长度 | ||
| C. | 向左平移$\frac{π}{6}$个单位长度 | D. | 向左平移$\frac{π}{12}$个单位长度 |
分析 由函数的最值求出A,由周期求出ω,由五点法作图求出φ的值,可得函数的解析式,再根据y=Asin(ωx+φ)的图象变换规律,可得结论.
解答 解:由函数f(x)=Asin(ωx+φ)的图象可得A=1,
根据$\frac{T}{4}$=$\frac{1}{4}$$•\frac{2π}{ω}$=$\frac{7π}{12}$-$\frac{π}{3}$,求得ω=2,
再根据五点法作图可得2×$\frac{π}{3}$+φ=π,求得φ=$\frac{π}{3}$,
∴f(x)=sin(2x+$\frac{π}{3}$)=sin2(x+$\frac{π}{6}$),
∵g(x)=sin(2x+$\frac{π}{2}$)=sin2(x+$\frac{π}{4}$)=sin2(x+$\frac{π}{6}$+$\frac{π}{12}$)=f(x+$\frac{π}{12}$),
∴把f(x)的图象向左平移$\frac{π}{12}$个单位长度,可得g(x)的图象,
故选:D.
点评 本题主要考查利用y=Asin(ωx+φ)的图象特征,由函数y=Asin(ωx+φ)的部分图象求解析式,y=Asin(ωx+φ)的图象变换规律,属于基础题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
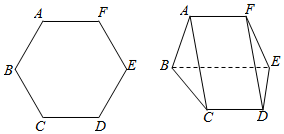 如图,将边长为2的正六边形ABCDEF沿对角线BE翻折,连接AC、FD,形成如图所示的多面体,且AC=$\sqrt{6}$,
如图,将边长为2的正六边形ABCDEF沿对角线BE翻折,连接AC、FD,形成如图所示的多面体,且AC=$\sqrt{6}$,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
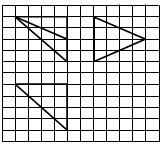
 一个正三棱柱的侧棱长与底面边长相等,表面积为12+2$\sqrt{3}$,它的三视图中,俯视图如图所示,侧视图是一个矩形,则正三棱柱绕上、下底面中心连线旋转30°后的正视图面积为( )
一个正三棱柱的侧棱长与底面边长相等,表面积为12+2$\sqrt{3}$,它的三视图中,俯视图如图所示,侧视图是一个矩形,则正三棱柱绕上、下底面中心连线旋转30°后的正视图面积为( )| A. | 4 | B. | 2$\sqrt{3}$ | C. | 2 | D. | $\frac{4\sqrt{3}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{32}{3}$ | B. | $\frac{64}{3}$ | C. | 32 | D. | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-3,+∞) | B. | (-∞,-$\frac{1}{3}$] | C. | [$\frac{1}{3}$,+∞) | D. | (-∞,$\frac{1}{3}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2,2$\sqrt{2}$) | B. | (2$\sqrt{3}$,2) | C. | (2,2$\sqrt{3}$) | D. | (2$\sqrt{2}$,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“?x∈R,x+3>0”的否定是“?x∈R,x+3<0” | |
| B. | 命题“若α=$\frac{π}{3}$,则cosα=$\frac{1}{2}$”的否命题是“若α=$\frac{π}{3}$,则cosα≠$\frac{1}{2}$” | |
| C. | 在区间[-1,1]上随机取一个数x,则事件“2x≤$\sqrt{2}$”发生的概率为$\frac{1}{4}$ | |
| D. | “命题p∧q为真”是“命题p∨q为真”的充分不必要条件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com