
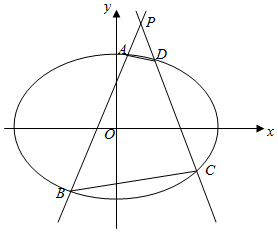
 如图,在平面直角坐标系xOy中,已知椭圆Γ:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左、右焦点分别为F1(-$\sqrt{3}$,0),F2($\sqrt{3}$,0),且椭圆Γ的上顶点到直线$\sqrt{3}$x+y+1=0的距离等于1.
如图,在平面直角坐标系xOy中,已知椭圆Γ:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左、右焦点分别为F1(-$\sqrt{3}$,0),F2($\sqrt{3}$,0),且椭圆Γ的上顶点到直线$\sqrt{3}$x+y+1=0的距离等于1.分析 (1)椭圆上顶点(0,b),由题意可得:$\frac{b+1}{2}$=1,c=$\sqrt{3}$,a2=b2+c2.联立解出即可得出.
(2)设直线l1的斜率为k,则l2的斜率为-k.A(x1,y1),B(x2,y2),C(x3,y3),D(x4,y4).直线l1,l2的方程分别为:y-2=k(x-1),y-2=-k(x-1),分别与椭圆的方程联立,利用根与系数的关系及其斜率计算公式即可得出.
解答 解:(1)椭圆上顶点(0,b),由题意可得:$\frac{b+1}{2}$=1,c=$\sqrt{3}$,a2=b2+c2.
联立解得b=1,a=2.
∴椭圆的标准方程为:$\frac{{x}^{2}}{4}+{y}^{2}$=1.
(2)设直线l1的斜率为k,则l2的斜率为-k.A(x1,y1),B(x2,y2),C(x3,y3),D(x4,y4).
直线l1,l2的方程分别为:y-2=k(x-1),y-2=-k(x-1),
联立$\left\{\begin{array}{l}{y=kx+2-k}\\{\frac{{x}^{2}}{4}+{y}^{2}=1}\end{array}\right.$,化为:(1+4k2)x2+(16k-8k2)x+4k2-16k+12=0,
△>0,
∴x1+x2=$\frac{8{k}^{2}-16k}{1+4{k}^{2}}$,x1x2=$\frac{4{k}^{2}-16k+12}{1+4{k}^{2}}$,
同理可得:x3+x4=$\frac{8{k}^{2}+16k}{1+4{k}^{2}}$,x3,x4=$\frac{4{k}^{2}+16k+12}{1+4{k}^{2}}$,
∴kAC+kBD=$\frac{{y}_{3}-{y}_{1}}{{x}_{3}-{x}_{1}}$+$\frac{{y}_{4}-{y}_{2}}{{x}_{4}-{x}_{2}}$=$\frac{-k{x}_{3}+2+k-(k{x}_{1}+2-k)}{{x}_{3}-{x}_{1}}$+$\frac{-k{x}_{4}+k+2-(k{x}_{2}+2-k)}{{x}_{4}-{x}_{2}}$
=$\frac{-k({x}_{3}+{x}_{1}-2)}{{x}_{3}-{x}_{1}}$+$\frac{-k({x}_{4}+{x}_{2}-2)}{{x}_{4}-{x}_{2}}$
=$\frac{-2k[{x}_{3}{x}_{4}-{x}_{1}{x}_{2}+({x}_{1}+{x}_{2})-({x}_{3}+{x}_{4})]}{({x}_{3}-{x}_{1})({x}_{4}-{x}_{2})}$,
分子=-2k$[\frac{4{k}^{2}+16k+12}{1+4{k}^{2}}-\frac{4{k}^{2}-16k+12}{1+4{k}^{2}}$-$\frac{8{k}^{2}+16k}{1+4{k}^{2}}$+$\frac{8{k}^{2}-16k}{1+4{k}^{2}}]$
=0.
∴kAC+kBD=0.
点评 本题考查了椭圆的标准方程及其性质、直线与椭圆相交问题、一元二次方程的根与系数的关系、斜率计算公式,考查了推理能力与计算能力,属于难题.


科目:高中数学 来源: 题型:选择题
| A. | 40人 | B. | 60人 | C. | 80人 | D. | 20人 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知函数 f(x)=Acos(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.
已知函数 f(x)=Acos(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 10 | B. | 20 | C. | 40 | D. | 60 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 面对全球范围内日益严峻的能源形势与环保压力,环保与低碳成为今后汽车发展的一大趋势,越来越多的消费者对新能源汽车表示出更多的关注,某研究机构从汽车市场上随机抽取N辆纯电动汽车调查其续航里程(单次充电后能行驶的最大里程),被调查汽车的续航里程全部介于100公里和450公里之间,根据调查数据形成了如图所示频率分布表及频率分布直方图.
面对全球范围内日益严峻的能源形势与环保压力,环保与低碳成为今后汽车发展的一大趋势,越来越多的消费者对新能源汽车表示出更多的关注,某研究机构从汽车市场上随机抽取N辆纯电动汽车调查其续航里程(单次充电后能行驶的最大里程),被调查汽车的续航里程全部介于100公里和450公里之间,根据调查数据形成了如图所示频率分布表及频率分布直方图.| 分组 | 频数 | 频率 |
| [100,150) | 1 | 0.05 |
| [150,200) | 3 | 0.15 |
| [200,250) | x | 0.1 |
| [250,300) | 6 | 0.3 |
| [300,350) | 4 | 0.2 |
| [350,400) | 3 | y |
| [400,450] | 1 | 0.05 |
| 合计 | N | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{6}$ | B. | $\sqrt{2}$ | C. | 1 | D. | $\frac{{\sqrt{2}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 设函数$f(x)=cos(ωx+φ)(ω>0,-\frac{π}{2}<φ<0)$的最小正周期为π,且$f(\frac{π}{4})=\frac{{\sqrt{3}}}{2}$.
设函数$f(x)=cos(ωx+φ)(ω>0,-\frac{π}{2}<φ<0)$的最小正周期为π,且$f(\frac{π}{4})=\frac{{\sqrt{3}}}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com