练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    10．为了解高一年级1200名学生的视力情况，采用系统抽样的方法，从中抽取容量为60的样本，则分段间隔为（　　）
    A．10B．20C．40D．60

    分析 利用系统抽样定义直接求解．

    解答 解：为了解高一年级1200名学生的视力情况，
    采用系统抽样的方法，从中抽取容量为60的样本，
    则分段间隔为：$\frac{1200}{60}$=20．
    故选：B．

    点评 本题考查抽样分段间隔的求法，是基础题，解题是要认真审题，注意系统抽样定义的合理运用．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    20．某校高一年级某次数学竞赛随机抽取100名学生的成绩，分组为[50，60），[60，70），[70，80），[80，90），[90，100]，统计后得到频率分布直方图如图所示：
    （1）试估计这组样本数据的众数和中位数（结果精确到0.1）；
    （2）年级决定在成绩[70，100]中用分层抽样抽取6人组成一个调研小组，对高一年级学生课外学习数学的情况做一个调查，则在[70，80），[80，90），[90，100]这三组分别抽取了多少人？
    （3）现在要从（2）中抽取的6人中选出正副2个小组长，求成绩在[80，90）中至少有1人当选为正、副小组长的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    1．已知某商品的进货单价为1元/件，商户甲往年以单价2元/件销售该商品时，年销量为1万件，今年拟下调销售单价以提高销量增加收益．据估算，若今年的实际销售单价为x元/件（1≤x≤2），则新增的年销量P=4（2-x）2（万件）．
    （1）写出今年商户甲的收益f（x）（单位：万元）与x的函数关系式；
    （2）商户甲今年采取降低单价提高销量的营销策略，是否能获得比往年更大的收益（即比往年收益更多）？请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．设p是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{9}$=1上一点，双曲线的一条渐近线方程为3x-2y=0，F1，F2分别是双曲线的左、右焦点，若|PF1|=5，则|PF2|=（　　）
    A．1或5B．1或9C．1D．9

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    5．设α，β是两个不同的平面，m，n，l 是三条不同的直线，下列命题中正确的是（　　）
    A．若α∩β=l，m?α，n?β，则m，n一定相交B．若α∥β，m?α，n?β，则m，n一定平行
    C．若α∥β，m∥α，n∥β，则m，n一定平行D．若α⊥β，m⊥α，n⊥β，则m，n一定垂直

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）右焦点为F，右顶点为A，一条渐近线方程为y=2$\sqrt{2}$x，且|AF|=2，则该双曲线的实轴长为（　　）
    A．4B．2$\sqrt{3}$C．2$\sqrt{2}$D．2

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

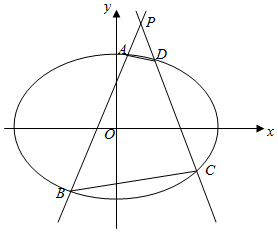    2．如图，在平面直角坐标系xOy中，已知椭圆Γ：$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0）的左、右焦点分别为F1（-$\sqrt{3}$，0），F2（$\sqrt{3}$，0），且椭圆Γ的上顶点到直线$\sqrt{3}$x+y+1=0的距离等于1．
    （1）求椭圆Γ的标准方程；
    （2）过点P（1，2）作两条倾斜角互补的两直线l1，l2分别交椭圆Γ于A，B，C，D四点，求kAC+kBD的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    19．若等比数列{an}的前n项和Sn=3n-1，则其公比为（　　）
    A．-3B．3C．-1D．1

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    20．已知m、n为两条不同的直线，α、β、γ为三个不同的平面，下列结论正确的是（　　）
    A．若m∥α，n∥α，则m∥nB．若α∥γ，β∥γ，则α∥β
    C．若α⊥β，m∥α，则m⊥βD．若α⊥β，m?α，n?β，则m⊥n

    查看答案和解析>>

    同步练习册答案