
分析 (1)由已知整理可得:c2+b2-a2=bc,利用余弦定理可求cosA=$\frac{1}{2}$,结合范围A∈(0,π),可求A的值.
(2)由三角形面积公式可求bc=8,结合余弦定理可求b+c=6,联立即可解得b,c的值.
解答 (本题满分为12分)
解:(1)∵bc=a2-(b-c)2,整理可得:c2+b2-a2=bc,…2分
∴cosA=$\frac{1}{2}$,…4分
∵A∈(0,π),
∴A=$\frac{π}{3}$…6分
(2)∵a=2$\sqrt{3}$,及(1)可得:12=b2+c2-bc=(b+c)2-3bc,…8分
又∵S=$\frac{1}{2}$bcsinA=2$\sqrt{3}$,可得:bc=8,…10分
∴b+c=6,
∴解得:$\left\{\begin{array}{l}{b=4}\\{c=2}\end{array}\right.$,或$\left\{\begin{array}{l}{b=2}\\{c=4}\end{array}\right.$.…12分
点评 本题主要考查了余弦定理,三角形面积公式在解三角形中的应用,考查了转化思想,属于基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{2}{5}$ | D. | $\frac{1}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x∈R,cosx≥1 | B. | ?x∈R,cosx>1 | C. | ?x0∈R,cosx0≥1 | D. | ?x0∈R,cosx0>1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若m∥α,α∩β=n,则 m∥n | B. | 若m∥α,m⊥n,则n⊥α | ||
| C. | 若m⊥α,n⊥α,则m∥n | D. | 若m?α,n?β,α⊥β,则m⊥n |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
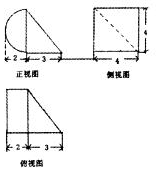
| A. | 4π+8 | B. | 8π+16 | C. | 16π+16 | D. | 16π+48 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | c>b>a | B. | c>a>b | C. | a>b>c | D. | b>c>a |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 事件A的概率P(A)必有0<P(A)<1 | |
| B. | 事件A的概率P(A)=0.999,则事件A是必然事件 | |
| C. | 用某种药物对患有胃溃疡的500名病人治疗,结果有380人有明显的疗效,现有胃溃疡的病人服用此药,则估计其有明显的疗效的可能性为76% | |
| D. | 某奖券中奖率为50%,则某人购买此券10张,一定有5张中奖 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com