考点:其他不等式的解法,利用导数求闭区间上函数的最值
专题:导数的综合应用
分析:(Ⅰ)利用导数判断知,当x=0时,g(x)在x=0时取得极小值,也是最小值;
(Ⅱ)依题意可得2x-m>x(ex-x),整理得m<-x(ex-x-2),令h(x)=-x(ex-x-2)(x>0),利用导数法可求得h(x)max,从而可得m的取值范围.
解答:
解:(Ⅰ)g′(x)=e
x-1,
当x>0时,g′(x)>0,g(x)=e
x-x在区间(0,+∞)上单调递增;
当x<0时,g′(x)<0,g(x)=e
x-x在区间(-∞,0)上单调递减;
∴当x=0时,g(x)在x=0时取得极小值,也是最小值,即g(x)
min=g(0)=1.
(Ⅱ)∵g(x)≥1,∴
>x?2x-m>x(e
x-x),
∴m<-x(e
x-x-2),
令h(x)=-x(e
x-x-2)(x>0),
则h′(x)=-(e
x-x-2)-x(e
x-1)=(x+1)(2-e
x),
当0<x<ln2时,h′(x)>0;当x>ln2时,h′(x)<0;
∴当x=ln2时,h(x)取得极大值,也是最大值,为h(ln2)=-ln2(e
ln2-ln2-2)=ln
22.
∴m<ln
22.
点评:本题考查利用导数求闭区间上函数的最值,考查导数的综合应用,考查等价转化思想与运算求解能力,属于中档题.



 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案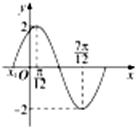 已知函数f(x)=Asin(ωx+φ)在一个周期内的图象如图所示.
已知函数f(x)=Asin(ωx+φ)在一个周期内的图象如图所示. 如图,三棱柱ABC-A1B1C1中,侧棱垂直底面,∠ACB=90°,AC=BC=
如图,三棱柱ABC-A1B1C1中,侧棱垂直底面,∠ACB=90°,AC=BC= 平行四边形ABCD中,BC=2,CD=
平行四边形ABCD中,BC=2,CD=