
分析 (1)要使函数$f(x)=\sqrt{x+3}+\frac{1}{x-2}$有意义,则$\left\{{\begin{array}{l}{x+3≥0}\\{x-2≠0}\end{array}}\right.$,由此能求出函数f(x)的定义域.
(2)由函数$f(x)=\sqrt{x+3}+\frac{1}{x-2}$,能求出f(1)+f(-3)的值.
(3)由函数$f(x)=\sqrt{x+3}+\frac{1}{x-2}$,能求出f(a+1)的值.
解答 解:(1)要使函数$f(x)=\sqrt{x+3}+\frac{1}{x-2}$有意义
则$\left\{{\begin{array}{l}{x+3≥0}\\{x-2≠0}\end{array}}\right.$--------(2分)
即x≥-3且x≠2,--------(4分)
∴函数f(x)的定义域为{x|x≥-3且x≠2}(区间表示也可以)--------(5分)
(2)∵函数$f(x)=\sqrt{x+3}+\frac{1}{x-2}$,
∴$f(1)=\sqrt{1+3}+\frac{1}{1-2}=2-1=1$--------(6分)
$f({-3})=\sqrt{-3+3}+\frac{1}{-3-2}=0-\frac{1}{5}=-\frac{1}{5}$-------(7分)
∴$f(1)+f({-3})=\frac{4}{5}$--------(8分)
(3)∵函数$f(x)=\sqrt{x+3}+\frac{1}{x-2}$,a>-4且a≠1,
∴f(a+1)=$\sqrt{a+1+3}+\frac{1}{a+1-2}$=$\sqrt{a+4}+\frac{1}{a-1}$.--------(10分)
点评 本题考查函数的定义域及函数值的求法,是基础题,解题时要认真审题,注意函数性质的合理运用.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-8,16] | B. | (-∞,-8]∪[16,+∞) | C. | (-∞,-8)∪(16,+∞) | D. | [16,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x∈R,x2-2x+1≥0 | B. | ?x∈R,x2-2x+1>0 | C. | ?x∈R,x2-2x+1≥0 | D. | ?x∈R,x2-2x+1<0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
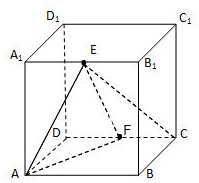 在棱长为2的正方体ABCD-A1B1C1D1中,E,F分别为A1B1,CD的中点.
在棱长为2的正方体ABCD-A1B1C1D1中,E,F分别为A1B1,CD的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com