
分析 (Ⅰ)当a=6时,分类讨论,去掉绝对值符号,即可求函数f(x)的值域;
(Ⅱ)设0<a≤4,分类讨论,去掉绝对值符号,利用对称轴和区间之间的关系求函数f(x)最小值g(a).
解答 解:(Ⅰ)当a=6时,$f(x)={x^2}-|6x-2|=\left\{\begin{array}{l}{x^2}+6x-2={(x+3)^2}-11,\;\;-1≤x<\frac{1}{3}\\{x^2}-6x+2={(x-3)^2}-7,\;\;\frac{1}{3}≤x<2\end{array}\right.$,
当$-1≤x<\frac{1}{3}$时,$f(x)∈[-7,\frac{1}{9}]$;
当$\frac{1}{3}≤x<2$时,$f(x)∈[-6,\frac{1}{9}]$,
函数f(x)的值域为$[-7,\frac{1}{9}]$.
(Ⅱ)$f(x)={x^2}-|ax-2|=\left\{\begin{array}{l}{x^2}+ax-2={(x+\frac{a}{2})^2}-\frac{a^2}{4}-2,\;\;x<\frac{2}{a}\\{x^2}-ax+2={(x-\frac{a}{2})^2}-\frac{a^2}{4}+2,\;\;x≥\frac{2}{a}\end{array}\right.$
(1)当0<a<1时,$\frac{2}{a}>2$,$-\frac{1}{2}<-\frac{a}{2}<0$,
此时当x∈[-1,2]时,f(x)=x2+ax-2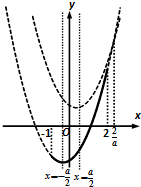
在$[-1,-\frac{a}{2}]$上单调递减,在$(-\frac{a}{2},2]$上单调递增,
所以$g(a)=f(-\frac{a}{2})=-\frac{a^2}{4}-2$;
(2)当1≤a≤2时,$\frac{2}{a}≥\frac{a}{2}$,$-1≤-\frac{a}{2}≤-\frac{1}{2}$f(x)在$[-1,-\frac{a}{2}]$上单调递减,在$(-\frac{a}{2},2]$上单调递增,
所以$g(a)=f(-\frac{a}{2})=-\frac{a^2}{4}-2$;
(3)当2<a≤4时,$\frac{2}{a}<\frac{a}{2}$,$-2≤-\frac{a}{2}<-1$f(x)在$[-1,\frac{2}{a}]$上单调递增,在$(\frac{2}{a},\frac{a}{2}]$上单调递减,
在$(\frac{a}{2},2]$上单调递增,所以$g(a)=min\{f(-1),f(\frac{a}{2})\}$,$f(-1)-f(\frac{a}{2})=(-a-1)-(-\frac{a^2}{4}+2)=\frac{1}{4}{(a-2)^2}-4<0$,
所以$f(-1)<f(\frac{a}{2})$,故g(a)=f(-1)=-a-1;
综上所述:$g(a)=\left\{\begin{array}{l}-\frac{a^2}{4}-2,\;\;0<a≤2\\-a-1,\;\;2<a≤4\end{array}\right.$.
点评 本题主要考查二次函数的图象和性质,要求熟练掌握对称轴和区间之间的关系.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(\sqrt{3}\;,\;\;2)$ | B. | (-3,2) | C. | (1,2) | D. | $(\sqrt{3}\;,\;\;\sqrt{5})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
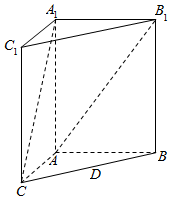 如图,在三棱柱ABC-A1B1C1中,四边形AA1C1C是边长为4的正方形,平面ABC⊥平面AA1C1C,AB=3,BC=5
如图,在三棱柱ABC-A1B1C1中,四边形AA1C1C是边长为4的正方形,平面ABC⊥平面AA1C1C,AB=3,BC=5查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{16}$π | B. | $\frac{3}{8}$π | C. | $\frac{3}{4}$π | D. | $\frac{3}{2}$π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1+e | B. | e-1 | C. | 1-e | D. | e |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com