
分析 (1)当m=1时,求得f(x)的解析式,求导,由f′(x)在(0,+∞)上单调递增,且f′(1)=0,即可求得函数f(x)的单调增区间;
(2)由题意构造辅助函数,h(x)=$\frac{f(x)}{x}$=$\frac{m}{{x}^{2}}$+lnx,φ(x)=$\frac{g(x)}{x}$=$\frac{lnx-2}{x}$,根据函数的单调性求得φ(x)∈[-2,-$\frac{1}{e}$],则h(x)∈[$\frac{1}{2}$,e],即$\frac{{x}^{2}}{2}$-x2lnx≤m≤x2(e-lnx),在[1,e]上恒成立,分别构造函数,求导,根据函数的单调性分别求得$\frac{{x}^{2}}{2}$-x2lnx最大值及x2(e-lnx)的最小值,即可求得实数m的取值范围.
解答 解:(1)当m=1时,数f(x)=$\frac{1}{m}$+xlnx,求导f′(x)=-$\frac{1}{{x}^{2}}$+lnx+1,
由f′(x)在(0,+∞)上单调递增,且f′(1)=0,
∴当x>1时,f′(x)>0,当0<x<1时,f′(x)<0,
∴函数f(x)单调递增区间(1,+∞);
(2)由题意设h(x)=$\frac{f(x)}{x}$=$\frac{m}{{x}^{2}}$+lnx,φ(x)=$\frac{g(x)}{x}$=$\frac{lnx-2}{x}$,
φ′(x)=$\frac{3-lnx}{{x}^{2}}$>0,在[1,e]恒成立
∴φ(x)=$\frac{lnx-2}{x}$在[1,e]上单调递增,φ(x)∈[-2,-$\frac{1}{e}$],
∴h(x)∈[$\frac{1}{2}$,e],即$\frac{1}{2}$≤$\frac{m}{{x}^{2}}$+lnx≤e,在[1,e]上恒成立,
即$\frac{{x}^{2}}{2}$-x2lnx≤m≤x2(e-lnx),在[1,e]上恒成立,
设p(x)=$\frac{{x}^{2}}{2}$-x2lnx,则p′(x)=-2xlnx≤0,在[1,e]上恒成立,
∴p(x)在[1,e]上单调递减,则m≥p(1)=$\frac{1}{2}$,
设q(x)=x2(e-lnx),q′(x)=x(2x-1-2lnx)≥x(2e-1-2lnx)>0在[1,e]上恒成立,
∴q(x)在[1,e]上单调递增,则m≤q(1)=e,
综上所述,m的取值范围[$\frac{1}{2}$,e].
点评 本题考查导数的综合应用,考查利用导数求函数的单调性及最值,考查不等式的恒成立问题,考查转化思想,属于中档题.


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | 24 | B. | 20 | C. | 16 | D. | 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [2,3] | B. | (-2,3] | C. | [1,2) | D. | (-∞,-2]∪[1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图所示的茎叶图记录了甲、乙两组各5名工人某日的产量数据(单位:件).若这两组数据的中位数相等,且平均值也相等,则x和y的值分别为( )
如图所示的茎叶图记录了甲、乙两组各5名工人某日的产量数据(单位:件).若这两组数据的中位数相等,且平均值也相等,则x和y的值分别为( )| A. | 3,5 | B. | 5,5 | C. | 3,7 | D. | 5,7 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
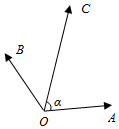 如图,在同一个平面内,向量$\overrightarrow{OA}$,$\overrightarrow{OB}$,$\overrightarrow{OC}$的模分别为1,1,$\sqrt{2}$,$\overrightarrow{OA}$与$\overrightarrow{OC}$的夹角为α,且tanα=7,$\overrightarrow{OB}$与$\overrightarrow{OC}$的夹角为45°.若$\overrightarrow{OC}$=m$\overrightarrow{OA}$+n$\overrightarrow{OB}$(m,n∈R),则m+n=3.
如图,在同一个平面内,向量$\overrightarrow{OA}$,$\overrightarrow{OB}$,$\overrightarrow{OC}$的模分别为1,1,$\sqrt{2}$,$\overrightarrow{OA}$与$\overrightarrow{OC}$的夹角为α,且tanα=7,$\overrightarrow{OB}$与$\overrightarrow{OC}$的夹角为45°.若$\overrightarrow{OC}$=m$\overrightarrow{OA}$+n$\overrightarrow{OB}$(m,n∈R),则m+n=3.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com