
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
分析 ①特殊情况当四点不在同一条直线上时才成立;
②根据三角函数线可判断正确;
③考虑当$\overrightarrow b$为零向量时的特殊情况;
④若$\frac{\overrightarrow a}{{|{\overrightarrow a}|}}$=$\frac{\overrightarrow b}{{|{\overrightarrow b}|}}$,则$\overrightarrow a$与$\overrightarrow b$为同向的共线向量,比如$\overrightarrow a$=3$\overrightarrow b$也成立等.
解答 解:①若$\overrightarrow{AD}$=$\overrightarrow{BC}$,当四点不在同一条直线上时,才有ABCD是平行四边形,故错误;
②cos$\frac{2}{7}$π<sin$\frac{5}{7}$π<tan$\frac{2}{7}$π
sin$\frac{5}{7}$π=sin$\frac{2}{7}$π>sin$\frac{π}{4}$,根据三角函数线可判断正确;
③若$\overrightarrow a$∥$\overrightarrow b$,$\overrightarrow b$∥$\overrightarrow c$,当$\overrightarrow b$为零向量时,不一定$\overrightarrow a$∥$\overrightarrow c$,故错误;
④若$\frac{\overrightarrow a}{{|{\overrightarrow a}|}}$=$\frac{\overrightarrow b}{{|{\overrightarrow b}|}}$,则$\overrightarrow a$与$\overrightarrow b$为同向的共线向量,但不一定相等,故错误.
故选B.
点评 考查了向量共线的定义和零向量与任意向量都共线和三角函数线的知识,属于基础题型,应熟练掌握.


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:高中数学 来源: 题型:解答题
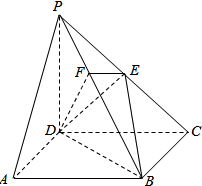 如图,在底面为正方形的四棱锥P-ABCD中,侧棱PD⊥底面ABCD,PD=DC,点E是线段PC的中点.
如图,在底面为正方形的四棱锥P-ABCD中,侧棱PD⊥底面ABCD,PD=DC,点E是线段PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,10) | B. | (1,+∞) | C. | (0,1) | D. | (10,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\sqrt{5}$,$\sqrt{13}$) | B. | (1,5) | C. | (1,$\sqrt{5}$) | D. | ($\sqrt{13}$,5) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a9>b9 | B. | a9=b9 | ||
| C. | a9<b9 | D. | a9与b9大小无法确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com