
分析 由$|\overrightarrow{a}-\overrightarrow{b}{|}^{2}=(\overrightarrow{a}-\overrightarrow{b})^{2}$,展开后代入数量积公式求得答案.
解答 解:∵|$\overrightarrow a$|=|$\overrightarrow b$|=1且$\overrightarrow a$与$\overrightarrow b$夹角为120°,
∴$|\overrightarrow{a}-\overrightarrow{b}{|}^{2}=(\overrightarrow{a}-\overrightarrow{b})^{2}=|\overrightarrow{a}{|}^{2}-2\overrightarrow{a}•\overrightarrow{b}+|\overrightarrow{b}{|}^{2}$
=1-2$|\overrightarrow{a}||\overrightarrow{b}|cos120°+1$=$2-2×1×1×(-\frac{1}{2})=3$,
∴$|\overrightarrow{a}-\overrightarrow{b}|=\sqrt{3}$.
点评 本题考查平面向量的数量积运算,考查向量模的求法,是基础题.


科目:高中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
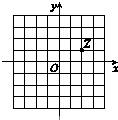 若i为虚数单位,图中网格纸的小正方形的边长是1,复平面内点Z表示复数z,则复数z的共轭复数是( )
若i为虚数单位,图中网格纸的小正方形的边长是1,复平面内点Z表示复数z,则复数z的共轭复数是( )| A. | 2+i | B. | 2-i | C. | 1+2i | D. | 1+2i |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| x | 2 | 4 | 5 | 6 | 8 |
| y | 30 | 40 | 60 | 50 | 70 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com