
分析 (I)奇数末尾是1,3,首位不能是0,可得奇数的个数;
(II)1和3不相邻,利用间接法;
(III)1不在万位,2不在个位,考虑1在个位与1不在个位,即可得出结论.
解答 解:(I)奇数末尾是1,3,首位不能是0,所以奇数共有${C^1}_2×{C^1}_3×{A^3}_3=36$个.…(3分)
(II)1和3不相邻,利用间接法,共有${C^1}_6×{A^2}_2×{A^3}_3-{C^1}_3×{A^2}_2×{A^2}_2=60$个.…(6分)
(III)1不在万位,2不在个位,考虑1在个位与1不在个位,共有${A^4}_4+{C^1}_2×{C^1}_3×{A^3}_3=60$个.…10分
点评 本题考查排列、组合的应用,解题中注意首位数字不能为0,一般需要分情况讨论.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:高中数学 来源: 题型:选择题
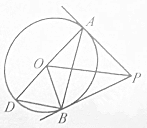 如图,点P在⊙O外,PA,PB切⊙O于A,B,AD为⊙O的直径,连结AB,OP,OB,BD,则图中与∠PAB相等的角有( )
如图,点P在⊙O外,PA,PB切⊙O于A,B,AD为⊙O的直径,连结AB,OP,OB,BD,则图中与∠PAB相等的角有( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | b>a>c | B. | c>a>b | C. | a>b>c | D. | c>b>a |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{55}$ | B. | 9 | C. | $\sqrt{91}$ | D. | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 某事件发生的概率为P(A)=1.1 | |
| B. | 不可能事件的概率为0,必然事件的概率为1 | |
| C. | 小概率事件就是不可能发生的事件,大概率事件就是必然要发生的事件 | |
| D. | 某事件发生的概率是随着试验次数的变化而变化的 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com