
| A. | $\sqrt{55}$ | B. | 9 | C. | $\sqrt{91}$ | D. | 10 |
分析 由条件利用两个向量的数量积的定义求得$\overrightarrow{a}•\overrightarrow{b}$,再根据|2$\overrightarrow a$-$\overrightarrow b}$|=$\sqrt{{(2\overrightarrow{a}-\overrightarrow{b})}^{2}}$,计算求得结果.
解答 解:平面向量$\overrightarrow a$与$\overrightarrow b$的夹角等于$\frac{5π}{6}$,如果|${\overrightarrow a}$|=4,|${\overrightarrow b}$|=$\sqrt{3}$,
∴$\overrightarrow{a}•\overrightarrow{b}$=4•$\sqrt{3}$•cos$\frac{5π}{6}$=-6,
∴|2$\overrightarrow a$-$\overrightarrow b}$|=$\sqrt{{(2\overrightarrow{a}-\overrightarrow{b})}^{2}}$=$\sqrt{{4\overrightarrow{a}}^{2}-4\overrightarrow{a}•\overrightarrow{b}{+\overrightarrow{b}}^{2}}$=$\sqrt{91}$,
故选:C.
点评 本题主要考查两个向量的数量积的定义,求向量的模的方法,属于基础题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
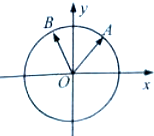 如图,在平面直角坐标系中,锐角α和钝角β的终边分别与单位圆交于A,B两点.
如图,在平面直角坐标系中,锐角α和钝角β的终边分别与单位圆交于A,B两点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
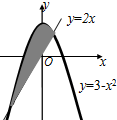
| A. | 10 | B. | $\frac{31}{3}$ | C. | 11 | D. | $\frac{32}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com