
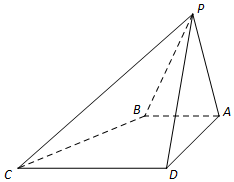
 如图四棱锥P-ABCD中,侧面PAD⊥底面ABCD.△PAD是正三角形,四边形ABCD是直角梯形,AB∥CD,AD=CD=2AB,点E为PD中点.
如图四棱锥P-ABCD中,侧面PAD⊥底面ABCD.△PAD是正三角形,四边形ABCD是直角梯形,AB∥CD,AD=CD=2AB,点E为PD中点.分析 (Ⅰ)由侧面PAD⊥底面ABCD,面PAD∩面ABCD=AD,可得CD⊥面PAD.
(Ⅱ)如图以AD的中点为原点,OD、OP方向分别为y轴、z轴建立坐标系,设AB=1,
则A(0,-1,0),D(0,1,0),P(0,0,$\sqrt{3}$),B(1,-1,0),C(2,1,0)
求出面PBC、面PDC的法向量,利用法向量垂直,得平面PBC⊥平面PCD.
(Ⅲ) 求出两个面的法向量,利用向量夹角公式求解.
解答 解:(Ⅰ)证明:∵四边形ABCD是直角梯形,AB∥CD,∴CD⊥AD,
∵侧面PAD⊥底面ABCD,面PAD∩面ABCD=AD,∴CD⊥面PAD.
(Ⅱ)证明:如图以AD的中点为原点,OD、OP方向分别为y轴、z轴建立坐标系,设AB=1,
则A(0,-1,0),D(0,1,0),P(0,0,$\sqrt{3}$),B(1,-1,0),C(2,1,0)
设面PBC的法向量为$\overrightarrow{m}=(x,y,z)$,$\overrightarrow{BC}=(1,2,0),\overrightarrow{BP}=(-1,1\sqrt{3})$.
由$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{BC}=x+2y=0}\\{\overrightarrow{m}•\overrightarrow{BP}=-x+y+\sqrt{3}z=0}\end{array}\right.$,可得$\overrightarrow{m}=(2,-1,\sqrt{3})$,
设面PDC的法向量为$\overrightarrow{n}=(a,b,c)$,由$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{DC}=2a=0}\\{\overrightarrow{n}•\overrightarrow{DP}=-b+\sqrt{3}c=0}\end{array}\right.$,可得$\overrightarrow{n}=(0,\sqrt{3,},1)$.
$\overrightarrow{m}•\overrightarrow{n}=2×0+(-1)×\sqrt{3}+\sqrt{3}×1=0$,∴平面PBC⊥平面PCD.
(Ⅲ)设面BDP的法向量为$\overrightarrow{d}=(e,f,h)$,$\overrightarrow{BD}=(-1,2,0)$.
由$\left\{\begin{array}{l}{\overrightarrow{d}•\overrightarrow{BD}=-e+2f=0}\\{\overrightarrow{d}•\overrightarrow{BP}=-e+f+\sqrt{3}h=0}\end{array}\right.$,可得$\overrightarrow{d}=(6,3,\sqrt{3})$,
cos$<\overrightarrow{m},\overrightarrow{d}>=\frac{\sqrt{6}}{4}$,二面角D-PB-C的余弦值为$\frac{\sqrt{6}}{4}$.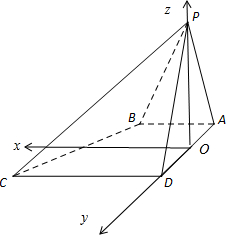
点评 本题考查了空间线面垂直、面面垂直,向量在空间问题中的应用,属于中档题.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:选择题
| A. | 函数$y=x+\frac{4}{x+1}$最小值为3 | B. | 函数$y=lgx+\frac{1}{lgx}$最小值为2 | ||
| C. | 函数$y={2^x}+\frac{1}{{{2^x}+1}}$最小值为1 | D. | 函数$y={x^2}+\frac{1}{x^2}$最小值为2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{4}$ | B. | $-\frac{3}{4}$ | C. | $\frac{4}{3}$ | D. | $-\frac{4}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-2,0] | B. | [-1,0] | C. | [-1,-2] | D. | [0,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com