
分析 (1)将不等式a2+b2≥2ab,a2+c2≥2ac,b2+c2≥2bc相加得出a2+b2+c2≥ab+ac+bc,再将a+b+c=1两边平方即可得出结论;
(2)$\frac{1}{a}+\frac{1}{b}+\frac{1}{c}$=(a+b+c)($\frac{1}{a}+\frac{1}{b}+\frac{1}{c}$),在利用基本不等式即可得出结论.
解答 证明:(1)∵a,b,c均为正数,
∴a2+b2≥2ab,a2+c2≥2ac,b2+c2≥2bc,
以上三式相加得:2(a2+b2+c2)≥2(ab+ac+bc),
∴a2+b2+c2≥ab+ac+bc;
∴(a+b+c)2=a2+b2+c2+2(ab+ac+bc)≥3(ab+bc+ac),
∵a+b+c=1,
∴1≥3(ab+bc+ac)
∴ab+bc+ca≤$\frac{1}{3}$(当且仅当a=b=c=$\frac{1}{3}$时取“=”).
(2)∵a,b,c均为正数,且a+b+c=1,
∴a+b+c≥3$\root{3}{abc}$,$\frac{1}{a}+\frac{1}{b}+\frac{1}{c}$≥3$\root{3}{\frac{1}{abc}}$,
∴$\frac{1}{a}+\frac{1}{b}+\frac{1}{c}$=(a+b+c)($\frac{1}{a}+\frac{1}{b}+\frac{1}{c}$)≥3$\root{3}{abc}$•3$\root{3}{\frac{1}{abc}}$=9.
当且仅当a=b=c=$\frac{1}{3}$时取“=”.
点评 本题考查了不等式的证明,基本不等式的应用,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
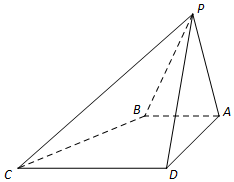 如图四棱锥P-ABCD中,侧面PAD⊥底面ABCD.△PAD是正三角形,四边形ABCD是直角梯形,AB∥CD,AD=CD=2AB,点E为PD中点.
如图四棱锥P-ABCD中,侧面PAD⊥底面ABCD.△PAD是正三角形,四边形ABCD是直角梯形,AB∥CD,AD=CD=2AB,点E为PD中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com