
分析 (Ⅰ)利用4Sn=(2n-1)an+1+1,写出4Sn-1=(2n-3)an+1,两式相减,得$\frac{{{a_{n+1}}}}{a_n}=\frac{2n+1}{2n-1}\;({n≥2})$,利用累加法求解an,判断数列{an}是首项为1,公差为2的等差数列.
(Ⅱ)利用放缩法以及裂项法,直接证明求解即可.
解答 (Ⅰ)证明:因为4Sn=(2n-1)an+1+1,所以当n≥2时,4Sn-1=(2n-3)an+1,
两式相减,得4an=(2n-1)an+1-(2n-3)an(n≥2),
所以(2n+1)an=(2n-1)an+1,即$\frac{{{a_{n+1}}}}{a_n}=\frac{2n+1}{2n-1}\;({n≥2})$,
在4Sn=(2n-1)an+1+1中,令n=1,得a2=3,
所以$\begin{array}{c}{a}_{n}=\frac{{a}_{n}}{{a}_{n-1}}•\frac{{a}_{n-1}}{{a}_{n-2}}•\frac{{a}_{n-2}}{{a}_{n-3}}•…•\frac{{a}_{3}}{{a}_{2}}•\frac{{a}_{2}}{{a}_{1}}•{a}_{1}\end{array}\right.$
=$\frac{2n-1}{2n-3}•\frac{2n-3}{2n-5}•\frac{2n-5}{2n-7}•…•\frac{5}{3}•\frac{3}{1}•1=2n-1$,
所以an-an-1=(2n-1)-(2n-3)=2(n≥2),
故数列{an}是首项为1,公差为2的等差数列,且an=2n-1.
(Ⅱ)解:由(Ⅰ)知,${S_n}=n+\frac{{n({n-1})}}{2}×2={n^2}$,
当n=1时,${T_1}=\frac{1}{{{a_1}\sqrt{S_1}}}=1<\frac{3}{2}$;
当n≥1时,${b_n}=\frac{1}{{{a_n}\sqrt{S_n}}}=\frac{1}{{({2n-1})n}}=\frac{2}{{2n({2n-1})}}<\frac{2}{{2n({2n-2})}}=\frac{1}{2n-2}-\frac{1}{2n}$,
所以${T_n}={b_1}+{b_2}+{b_3}+…+{b_n}<1+\frac{1}{2}-\frac{1}{4}+\frac{1}{4}-\frac{1}{6}+…+\frac{1}{2n-2}-\frac{1}{2n}=\frac{3}{2}-\frac{1}{2n}<\frac{3}{2}$.
点评 本题考查等差数列的判定,数列的递推关系式的应用,放缩法以及裂项求和的应用,考查分析问题解决问题的能力.


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\frac{4}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{8}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,+∞) | B. | (-∞,-1]∪[3,+∞) | C. | [-1,3] | D. | (-∞,3] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{{e}^{2π}(1-{e}^{2015π})}{1-{e}^{2π}}$ | B. | -$\frac{{e}^{2π}(1-{e}^{2015π)}}{1-{e}^{π}}$ | ||
| C. | -$\frac{1-{e}^{2016π}}{1-{e}^{2π}}$ | D. | -$\frac{{e}^{2π}(1-{e}^{2014π})}{1-{e}^{2π}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
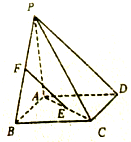 如图四棱锥P-ABCD的底面ABCD是菱形,PA⊥底面ABCD,E,F分别是AC,PB的中点,PA=AB=2,∠BAD=120°.
如图四棱锥P-ABCD的底面ABCD是菱形,PA⊥底面ABCD,E,F分别是AC,PB的中点,PA=AB=2,∠BAD=120°.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | c<b<a | B. | c<a<b | C. | b<a,c | D. | a<b<c |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
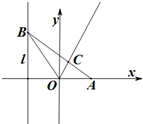 如图,已知定点A(1,0),点B是定直线l:x=-1上的动点,∠BOA的角平分线交AB于C.
如图,已知定点A(1,0),点B是定直线l:x=-1上的动点,∠BOA的角平分线交AB于C.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com