
【题目】已知λ,μ为常数,且为正整数,λ≠1,无穷数列{an}的各项均为正整数,其前n项和为Sn,对任意的正整数n,Sn=λan﹣μ.记数列{an}中任意两不同项的和构成的集合为A.
(1)证明:无穷数列{an}为等比数列,并求λ的值;
(2)若2015∈A,求μ的值;
(3)对任意的n∈N*,记集合Bn={x|3μ2n﹣1<x<3μ2n,x∈A}中元素的个数为bn,求数列{bn}的通项公式.
【答案】(1)见解析;
(2)31或403;
(3)bn=n(n∈N*)
【解析】
(1)证明:∵Sn=λan﹣μ.当n≥2时,Sn﹣1=λan﹣1﹣μ,
∴an=λan﹣λan﹣1,λ≠1,∴![]() ,
,
∴数列{an}为等比数列,
∵各项均为正整数,则公比![]() =
=![]() 为正整数,λ为正整数,
为正整数,λ为正整数,
∴λ=2.
(2)解:由(1)可得:Sn=2an﹣μ,当n=1时,a1=μ,则an=μ2n﹣1,
∴A={μ(2i﹣1+2j﹣1)|1≤i<j,i,j∈N*},
∵2015∈A,∴2015=μ(2i﹣1+2j﹣1)=μ2i﹣1(1+2j﹣i)=5×13×31,
∵j﹣i>0,则1+2j﹣i必为不小于3的奇数,
∵2i﹣1为偶数时,上式不成立,因此必有2i﹣1=1,∴i=1,
∴μ(1+2j﹣1)=5×13×31,
只有j=3,μ=403或j=7,μ=31时,上式才成立,
∴μ=31或403.
(3)解:当n≥1时,集合Bn={x|3μ2n﹣1<x<3μ2n,x∈A},
即3μ2n﹣1<μ(2i﹣1+2j﹣1)<3μ2n,1≤i<j,i,j∈N*.Bn中元素个数,
等价于满足3×2n<2i+2j<3×2n+1的不同解(i,j),
若j>n+2,则2i+2j≥2i+2n+3=2i+4×2n+1>3×2n+1,矛盾.
若j<n+2,则2i+2j≤2i+2n+1≤2n+2n+1=3×2n,矛盾.
∴j=n+2,又∵(21+2n+2)﹣3×2n=2+4×2n﹣3×2n=2+2n>0,
∴3×2n<21+2n+2<22+2n+2<…<2n+1+2n+2=3×2n+1,
即i=1,2,…,n时,共有n个不同的解(i,j),即共有n个不同的x∈Bn,
∴bn=n(n∈N*).


 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线l的参数方程为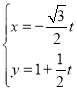 ,(t为参数)以坐标原点O为极点,以x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρ=2
,(t为参数)以坐标原点O为极点,以x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρ=2![]() sinθ,
sinθ,
(1)求直线l的普通方程及曲线C的直角坐标方程;
(2)直线l与x轴交于点P,与曲线C交于A,B两点,求|PA|+|PB|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】祖暅原理“幂势既同,则积不容异”中的“幂”指面积,“势”即是高,意思是:若两个等高的几何体在所有等高处的水平截面的面积恒等,则这两几何体的体积相等.设夹在两个平行平面之间的几何体的体积分别为![]() ,它们被平行于这两个平面的任意平面截得的两个截面面积分别为
,它们被平行于这两个平面的任意平面截得的两个截面面积分别为![]() ,则“
,则“![]() 恒成立”是“
恒成立”是“![]() ”的( )
”的( )
A.充分不必要条件B.必要不充分条件
C.充要条件D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)设θ∈[0,π],且f(θ)![]() 1,求θ的值;
1,求θ的值;
(2)在△ABC中,AB=1,f(C)![]() 1,且△ABC的面积为
1,且△ABC的面积为![]() ,求sinA+sinB的值.
,求sinA+sinB的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知顶点是坐标原点的抛物线![]() 的焦点
的焦点![]() 在
在![]() 轴正半轴上,圆心在直线
轴正半轴上,圆心在直线![]() 上的圆
上的圆![]() 与
与![]() 轴相切,且
轴相切,且![]() 关于点
关于点![]() 对称.
对称.
(1)求![]() 和
和![]() 的标准方程;
的标准方程;
(2)过点![]() 的直线
的直线![]() 与
与![]() 交于
交于![]() ,与
,与![]() 交于
交于![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校为了调查学生的学习情况,由每班随机抽取![]() 名学生进行调查,若一班有
名学生进行调查,若一班有![]() 名学生,将每一学生编号从
名学生,将每一学生编号从![]() 到
到![]() ,请从随机数表的第
,请从随机数表的第![]() 行第
行第![]() 、
、![]() 列(下表为随机数表的前
列(下表为随机数表的前![]() 行)开始,依次向右,直到取足样本,则第五个编号为_________.
行)开始,依次向右,直到取足样本,则第五个编号为_________.
7816 | 6514 | 0802 | 6314 | 0702 | 4369 | 9728 | 0198 |
3204 | 9234 | 4935 | 8200 | 3623 | 4869 | 6938 | 7481 |
7816 | 6514 | 0802 | 6314 | 0702 | 4369 | 9728 | 0198 |
3204 | 9234 | 4935 | 8200 | 3623 | 4869 | 6938 | 7481 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com