
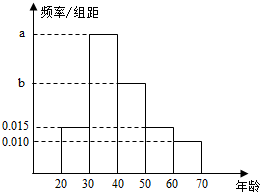
 根据某电子商务平台的调查统计显示,参与调查的1000位上网购物者的年龄情况如图显示.
根据某电子商务平台的调查统计显示,参与调查的1000位上网购物者的年龄情况如图显示.
|
| 3 |
| 5 |


科目:高中数学 来源: 题型:
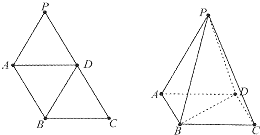 如图,在菱形ABCD中,AB=BD=2,三角形PAD为等边三角形,将它沿AD折成大小为α(
如图,在菱形ABCD中,AB=BD=2,三角形PAD为等边三角形,将它沿AD折成大小为α(| π |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| ||
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、从6名同学中,选出4名参加学校文艺汇演,每个人被选中的可能性大小 |
| B、同时掷两枚骰子,点数和为7的概率 |
| C、近三天中有一天降雪的概率 |
| D、3个人站成一排,其中甲,乙相邻的概率 |
查看答案和解析>>
科目:高中数学 来源: 题型:
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com