
分析 利用二项展开式的通项公式,二项式系数的性质,求得第10项、常数项、以及系数的绝对值最大的项.
解答 解 由题意得22n-2n=992,解得n=5,
∵(2x-$\frac{1}{x}$)2n的展开式的通项公式为 ${T_{r+1}}=C_{10}^r{(2x)^{10-r}}{(-\frac{1}{x})^r}=C_{10}^r{2^{10-r}}{(-1)^r}{x^{10-2r}}$,
(1 )令r=9,可得它的展开式中第10项,即T10=-20x-8 .
(2)令10-2r=0,求得r=5,可得常数项为第6项,
T6=-${C}_{10}^{5}$•25=-8 064.
(3)设第r+1项的系数的绝对值最大,即Tr+1=${C}_{10}^{r}$•210-r 最大,
∴$\left\{\begin{array}{l}{{C}_{10}^{r}{•2}^{10-r}{≥C}_{10}^{r-1}{•2}^{11-r}}\\{{C}_{10}^{r}{•2}^{10-r}{≥C}_{10}^{r+1}{•2}^{9-r}}\end{array}\right.$,即$\left\{\begin{array}{l}{11-r≥2r}\\{2(r+1)≥10-r}\end{array}\right.$,
∴$\frac{8}{3}$≤r≤$\frac{11}{3}$,∴r=3,故系数的绝对值最大的是第4项,
T4=(-1)3•${C}_{10}^{3}$•27•x4=-15 360x4.
点评 本题主要考查二项式定理的应用,二项展开式的通项公式,求展开式中某项的系数,二项式系数的性质,属于基础题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 10 | C. | 20 | D. | -20 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
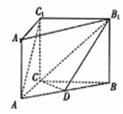 如图,在直三棱柱ABC-A1B1C1中,AC=3,BC=4,AA1=2,AC⊥BC,D是线段AB上一点.
如图,在直三棱柱ABC-A1B1C1中,AC=3,BC=4,AA1=2,AC⊥BC,D是线段AB上一点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{5}{2}$i | B. | -$\frac{5}{2}$ | C. | $\frac{5}{2}$i | D. | $\frac{5}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x<2} | B. | {x|x≤2} | C. | {x|2<x≤3} | D. | {x|2≤x<3} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\sqrt{5}$ | C. | $\sqrt{10}$ | D. | 2$\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com