
分析 两个单位立方体构成直二面角,建立空间坐标系,利用向量法能求出结果.
解答 解:如图为两个单位立方体构成,图中的左侧面和底面构成题目中的直二面角,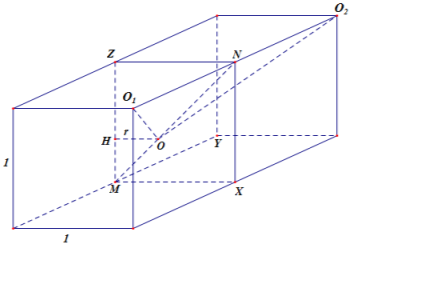
O1、O2为单位球的球心,小球O在MN上.
设OH=r,则有:OO1=OO2=r+1,才能满足外切条件.
如图,为M为原点建立空间坐标系,各点坐标为:
O (r,0,r),O2(1,1,1)
∴OO22=(1+r)2,(1-r)2+1+(1-r)2=(1+r)2,
解得:r=3±$\sqrt{7}$,
其中r=3-$\sqrt{7}$为符合题意的解.
∴r=3-$\sqrt{7}$.
故答案为:3-$\sqrt{7}$.
点评 本题考查小球半径的求法,是中档题,解题时要认真审题,注意向量法的合理运用.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 37 | B. | 38 | C. | 39 | D. | 40 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com