
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
分析 由平面向量坐标运算法则先分别求出$\overrightarrow{m},\overrightarrow{n}$,再由$\overrightarrow{m}$⊥$\overrightarrow{n}$,能求出实数λ.
解答 解:∵量$\overrightarrow{a}$=(1,-2),$\overrightarrow{b}$=(1,1),
∴$\overrightarrow{m}$=$\overrightarrow{a}$+$\overrightarrow{b}$=(2,-1),
$\overrightarrow{n}$=$\overrightarrow{a}$-λ$\overrightarrow{b}$=(1-λ,-2-λ),
∵$\overrightarrow{m}$⊥$\overrightarrow{n}$,∴$\overrightarrow{m}•\overrightarrow{n}$=2(1-λ)+(-1)(-2-λ)=0,
解得实数λ=4.
故选:A.
点评 本题考查实数值的求法,涉及到平面向量坐标运算法则、向量垂直的性质的应用等基础知识,考查推理论证能力、运算求解能力,考查函数与方程思想,是基础题.


科目:高中数学 来源: 题型:选择题
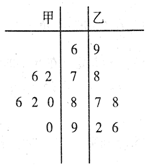 甲、乙两名学生的六次数学测试成绩(百分制)如图所示.
甲、乙两名学生的六次数学测试成绩(百分制)如图所示.| A. | ③④ | B. | ①② | C. | ②④ | D. | ①③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{3}$ | B. | $\frac{{\sqrt{21}}}{3}$ | C. | $\frac{5}{4}$ | D. | $\frac{{\sqrt{7}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | $3\sqrt{2}$ | C. | $\frac{3}{2}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,1] | B. | $[{-\sqrt{3},\sqrt{3}}]$ | C. | (-∞,-1]∪[1,+∞) | D. | [-$\sqrt{3}$,-1]∪[1,$\sqrt{3}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
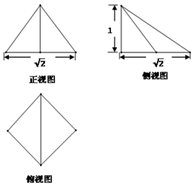 如图是一个简单几何体的三视图,则该几何体的体积为( )
如图是一个简单几何体的三视图,则该几何体的体积为( )| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com