练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    1．已知向量$\vec a=（2，-3，1），\vec b=（-4，2，x）$，且$\vec a⊥\vec b$，则x的值为（　　）
    A．12B．10C．-14D．14

    分析 利用空间向量的数量积公式以及向量垂直的性质得到关于x的方程解之即可．

    解答 解：因为向量$\vec a=（2，-3，1），\vec b=（-4，2，x）$，且$\vec a⊥\vec b$，
    属于$\overrightarrow{a}•\overrightarrow{b}$=-8-6+x=0，解得x=14；
    故选：D．

    点评 本题考查了空间向量的数量积以及向量垂直的性质；属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    11．命题“不等式x2+x-6＞0的解为x＜-3或x＞2”的逆否命题是若x≥-3且x≤2，则x2+x-6≤0．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

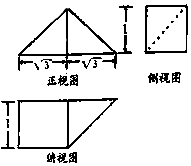    12．《九章算术》中，将底面是直角三角形的直三棱柱称之为“堑堵”，将底面为矩形，一条侧棱垂直于底面的四棱锥称之为“阳马”，已知某“堑堵”与某“阳马”组合而成的几何体的三视图如图所示，则该几何体的体积（　　）
    A．$\frac{{5\sqrt{3}}}{6}$B．$\frac{{7\sqrt{3}}}{6}$C．$\frac{{\sqrt{3}}}{6}$D．$\frac{{3\sqrt{3}}}{6}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

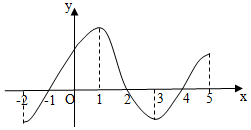    9．如图是函数y=f（x）的导数的图象，则正确的判断是（2）（4）．
    （1）f（x）在（-2，1）上是增函数；
    （2）x=-1是f（x）的极小值点；
    （3）x=2是f（x）的极小值点；
    （4）f（x）在（2，4）上是减函数，在（-1，2）上是增函数．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    16．若${（{x^2}-\frac{1}{x}）^n}$的展开式中含x3的项为第6项，设（1-3x）n=a0+a1x+a2x2+…+anxn，则a1+a2+…+an的值为-513．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．已知y=x•f'（x）的图象如图所示，则f（x）的一个可能图象是（　　）
    A．B．C．D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

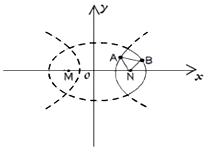    13．有一凸透镜其剖面图（如图）是由椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1和双曲线$\frac{{x}^{2}}{{m}^{2}}$-$\frac{{y}^{2}}{{n}^{2}}$=1（a＞m＞0）的实线部分组成，已知两曲线有共同焦点M、N；A、B分别在左右两部分实线上运动，则△ANB周长的最小值为（　　）
    A．2（a-m）B．（a-m）C．2（b-n）D．2（a+m）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．F1，F2分别是双曲线x2-$\frac{{y}^{2}}{{b}^{2}}$=1（b＞0）的左、右焦点，过F2的直线l与双曲线的左右两支分别交于A，B两点，若△ABF1是等边三角形，则该双曲线的虚轴长为（　　）
    A．2$\sqrt{6}$B．2$\sqrt{2}$C．$\sqrt{6}$D．4$\sqrt{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．各项均为正数的等比数列{an}的前n项和为Sn，若S4=10，S12=130，则S8=（　　）
    A．-30B．40C．40或-30D．40或-50

    查看答案和解析>>

    同步练习册答案