
分析 (Ⅰ)由点A(1,$\sqrt{2}$)是离心率为$\frac{\sqrt{2}}{2}$的椭圆C:$\frac{x^2}{b^2}+\frac{y^2}{a^2}=1$(a>b>0)上的一点,列出方程组求出a=2,$b=\sqrt{2}$,由此能求出椭圆C的方程.
(Ⅱ)设D(x1,y1),B(x2,y2),直线AB、AD的斜率分别为:kAB、kAD,设直线BD的方程为$y=\sqrt{2}x+b$,联立$\left\{{\begin{array}{l}{y=\sqrt{2}x+b}\\{2{x^2}+{y^2}=4}\end{array}}\right.$$,得4{x^2}+2\sqrt{2}bx+{b^2}-4=0$,由此利用根的判别式、韦达定理,结合已知条件能证明直线AB,AD的斜率之和为定值.
(Ⅲ)|BD|=$\sqrt{1+(\sqrt{2})^{2}}$|x1-x2|=$\frac{\sqrt{6}}{2}$$\sqrt{8-{b}^{2}}$,求出点A到直线BD:$y=\sqrt{2}x+b$的距离$d=\frac{|b|}{{\sqrt{3}}}$,由此能求出当b=±2时,△ABD的面积最大,最大值为$\sqrt{2}$.
解答 解:(Ⅰ)∵点A(1,$\sqrt{2}$)是离心率为$\frac{\sqrt{2}}{2}$的椭圆C:$\frac{x^2}{b^2}+\frac{y^2}{a^2}=1$(a>b>0)上的一点,
∴$\left\{\begin{array}{l}{e=\frac{c}{a}=\frac{\sqrt{2}}{2}}\\{\frac{1}{{b}^{2}}+\frac{2}{{a}^{2}}=1}\\{{a}^{2}={b}^{2}+{c}^{2}}\end{array}\right.$,解得a=2,$b=\sqrt{2}$,$c=\sqrt{2}$,
∴椭圆C的方程为$\frac{x^2}{2}+\frac{y^2}{4}=1$.…(2分)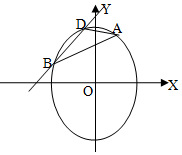
证明:(Ⅱ)设D(x1,y1),B(x2,y2),
直线AB、AD的斜率分别为:kAB、kAD,
则kAD+kAB=$\frac{{{y_1}-\sqrt{2}}}{{{x_1}-1}}+\frac{{{y_2}-\sqrt{2}}}{{{x_2}-1}}=\frac{{\sqrt{2}{x_1}+b-\sqrt{2}}}{{{x_1}-1}}+\frac{{\sqrt{2}{x_2}+b-\sqrt{2}}}{{{x_2}-1}}$
=$2\sqrt{2}+b[\frac{{{x_1}+{x_2}-2}}{{{x_1}{x_2}-({x_1}+{x_2})+1}}]$,(*)
设直线BD的方程为$y=\sqrt{2}x+b$,
联立$\left\{{\begin{array}{l}{y=\sqrt{2}x+b}\\{2{x^2}+{y^2}=4}\end{array}}\right.$$,得4{x^2}+2\sqrt{2}bx+{b^2}-4=0$,
∴△=-8b2+64>0,解得-2$\sqrt{2}$<b<2$\sqrt{2}$,${x_1}+{x_2}=-\frac{{\sqrt{2}}}{2}b$,----①,${x_1}{x_2}=\frac{{{b^2}-4}}{4}$-----②,
将①、②式代入*式整理得$2\sqrt{2}+b[\frac{{{x_1}+{x_2}-2}}{{{x_1}{x_2}-({x_1}+{x_2})+1}}]$=0,
∴kAD+kAB=0,∴直线AB,AD的斜率之和为定值.
解:(Ⅲ)|BD|=$\sqrt{1+(\sqrt{2})^{2}}$|x1-x2|=$\sqrt{3}$×$\frac{\sqrt{64-8{b}^{2}}}{4}$=$\frac{\sqrt{6}}{2}$$\sqrt{8-{b}^{2}}$,
设d为点A到直线BD:$y=\sqrt{2}x+b$的距离,∴$d=\frac{|b|}{{\sqrt{3}}}$,
∴${S_{△ABD}}=\frac{1}{2}|{BD}|d=\frac{{\sqrt{2}}}{4}\sqrt{(8-{b^2}){b^2}}≤\sqrt{2}$,
当且仅当b=±2时取等号,
∵±2$∈(-2\sqrt{2},2\sqrt{2})$,∴当b=±2时,△ABD的面积最大,最大值为$\sqrt{2}$.
点评 本题考查椭圆方程的求法,考查两直线的斜率之和为定值的证明,考查三角形面积是否有最大值的判断与求法,涉及到椭圆、直线方程、弦长公式、点到直线的距离公式、根的判别式、韦达定理等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | ∅ | B. | {x|0<x<1} | C. | {x|x<0} | D. | {x|x<1} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
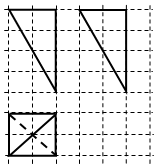 如图是某几何体的三视图,图中方格的单位长度为1,则该几何体外接球的直径为( )
如图是某几何体的三视图,图中方格的单位长度为1,则该几何体外接球的直径为( )| A. | $2\sqrt{2}$ | B. | $2\sqrt{3}$ | C. | $2\sqrt{6}$ | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
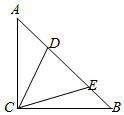 如图,等腰直角三角形区域ABC中,∠ACB=90°,BC=AC=1百米.现准备划出一块三角形区域CDE,其中D,E均在斜边AB上,且∠DCE=45°.记三角形CDE的面积为S.
如图,等腰直角三角形区域ABC中,∠ACB=90°,BC=AC=1百米.现准备划出一块三角形区域CDE,其中D,E均在斜边AB上,且∠DCE=45°.记三角形CDE的面积为S.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com