
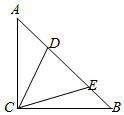
 如图,等腰直角三角形区域ABC中,∠ACB=90°,BC=AC=1百米.现准备划出一块三角形区域CDE,其中D,E均在斜边AB上,且∠DCE=45°.记三角形CDE的面积为S.
如图,等腰直角三角形区域ABC中,∠ACB=90°,BC=AC=1百米.现准备划出一块三角形区域CDE,其中D,E均在斜边AB上,且∠DCE=45°.记三角形CDE的面积为S.分析 (1)①等腰直角三角形区域ABC中,∠ACB=90°,BC=AC=100米,∠ACB=∠ABC=45°,由正弦定理表示CD和CE,即可用θ表示S;
②设AD=x,利用正弦定理把x与∠BCE=θ建立关系,带入①可得x表示S
(2)利用(1)中①的表达式,根据辅助角公式化简后,利用三角函数的有界限可得S的最大值.
解答 解:由题意,∠ACB=90°,BC=AC=100米,∠ACB=∠ABC=45°,
(1)①设∠BCE=θ(0≤θ≤45°),$∠CEB=π-\frac{π}{4}-θ=\frac{3π}{4}-θ$,$∠CDA=θ+\frac{π}{2}$.
在三角形ACD和三角形CBE中,由正弦定理:得:$\frac{CE}{sin45°}=\frac{1}{sin(\frac{3}{4}π-θ)}$
$\frac{CD}{sin45°}=\frac{1}{sin(θ+\frac{π}{2})}$
∴CE=$\frac{1}{sinθ+cosθ}$,CD=$\frac{\sqrt{2}}{2cosθ}$
那么:三角形CDE的面积为S=$\frac{1}{2}$CD•CE•sin45°=$\frac{1}{2}×$$\frac{1}{sinθ+cosθ}$×$\frac{\sqrt{2}}{2cosθ}$×$\frac{\sqrt{2}}{2}$=$\frac{1}{4sinθcosθ+4co{s}^{2}θ}$
②设AD=x,∠BCE=θ,那么∠ACD=$\frac{π}{4}$-θ.
在三角形ACD中,由正弦定理:得:$\frac{1}{sin(θ+\frac{π}{2})}=\frac{x}{sin(\frac{π}{4}-θ)}$
化简可得:x=$\frac{\sqrt{2}}{2}-\frac{\sqrt{2}}{2}tanθ$.
得:tanθ=1$-\sqrt{2}$x.
由①的表达式化简可得:S=$\frac{si{n}^{2}θ+co{s}^{2}θ}{4sinθcosθ+4co{s}^{2}θ}$=$\frac{ta{n}^{2}θ+1}{4tanθ+4}$
将tanθ=1$-\sqrt{2}$x带入上式,可得S=$\frac{(1-\sqrt{2}x)^{2}+1}{4(1-\sqrt{2}x)+4}$=$\frac{2{x}^{2}-2\sqrt{2}x+2}{4(2-\sqrt{2}x)}$=$\frac{{x}^{2}-\sqrt{2}x+1}{4-2\sqrt{2}x}$.
(2)由①的表达式S=$\frac{1}{4sinθcosθ+4co{s}^{2}θ}$
化简可得:S=$\frac{1}{2sin2θ+2(1+cos2θ)}$=$\frac{1}{2\sqrt{2}sin(2θ+\frac{π}{4})+2}$.
∵0≤θ≤45°,
∴$\frac{π}{4}≤2θ+\frac{π}{4}≤\frac{3π}{4}$.
可得:sin(2θ$+\frac{π}{4}$)∈[$\frac{\sqrt{2}}{2},1$].
∴Smax=$\frac{1}{2\sqrt{2}×\frac{\sqrt{2}}{2}+2}=\frac{1}{4}$.
点评 本题主要考查三角函数的图象和性质,利用三角函数公式将函数进行化简是解决本题的关键.属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | $\frac{1}{2}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $\frac{{\sqrt{2}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 144 | B. | 48 | C. | 24 | D. | 13 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {-1,0,1} | B. | {-2,-1,0,1} | C. | {0,1,2,3} | D. | {0,1,2} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 7 | B. | 8 | C. | 9 | D. | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a1+a9≥b1+b9 | B. | a1+a9≤b1+b9 | C. | a1+a9>b1+b9 | D. | a1+a9<b1+b9 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com