
| A. | 7 | B. | 8 | C. | 9 | D. | 10 |
分析 把已知函数式变形,根据条件可知b=0,然后根据三角函数的辅助角公式求函数的值域,再由最大值与最小值之和为6求得a的值,从而求得3a-2b的值.
解答 解:∵函数y=f(x)=a+$\frac{2bx+3sinx+bxcosx}{2+cosx}$=a+bx+$\frac{3sinx}{2+cosx}$有最大值和最小值,
∴必有b=0,
则y=f(x)=a+$\frac{3sinx}{2+cosx}$,即y-a=$\frac{3sinx}{2+cosx}$.
∴3sinx+(a-y)cosx=2y-2a,
得$\sqrt{9+(a-y)^{2}}sin(x+θ)=2y-2a$(tanθ=$\frac{a-y}{3}$).
∴sin(x+θ)=$\frac{2y-2a}{\sqrt{9+(a-y)^{2}}}$,
由|sin(x+φ)|=|$\frac{2y-2a}{\sqrt{9+(a-y)^{2}}}$|≤1,
可得(y-a)2≤3,故有a-$\sqrt{3}$≤y≤a+$\sqrt{3}$.
再根据最大值与最小值之和为6,可得2a=6,即a=3,
∴3a-2b=9-0=9,
故选:C.
点评 本题考查函数的最值及其几何意义,利用条件确定b=0是解决本题的关键,属于中档题.


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:高中数学 来源: 题型:解答题
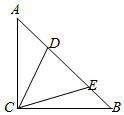 如图,等腰直角三角形区域ABC中,∠ACB=90°,BC=AC=1百米.现准备划出一块三角形区域CDE,其中D,E均在斜边AB上,且∠DCE=45°.记三角形CDE的面积为S.
如图,等腰直角三角形区域ABC中,∠ACB=90°,BC=AC=1百米.现准备划出一块三角形区域CDE,其中D,E均在斜边AB上,且∠DCE=45°.记三角形CDE的面积为S.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
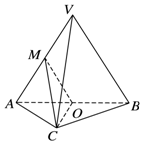 如图,在三棱锥VABC中,平面VAB⊥平面ABC,△VAB为等边三角形,AC⊥BC且AC=BC,O,M分别为AB,VA的中点.
如图,在三棱锥VABC中,平面VAB⊥平面ABC,△VAB为等边三角形,AC⊥BC且AC=BC,O,M分别为AB,VA的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x≤-1} | B. | {x|-1≤x≤0} | C. | {x|0≤x≤1} | D. | {x|1≤x≤2} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com