
分析 (1)利用导数,我们可以确定函数的单调性,这样就可求f(x)的极大值;(2)求导数,再进行类讨论,利用导数的正负,确定函数的单调性.
解答 解:(1)当m=2时,f(x)=$\frac{5}{2}$lnx+$\frac{1}{x}$-x,
f′(x)=-$\frac{(x-2)(2x-1)}{{2x}^{2}}$(x>0),
f′(x)<0,可得0<x<$\frac{1}{2}$或x>2;
令f′(x)>0,可得$\frac{1}{2}$<x<2,
∴f(x)在(0,$\frac{1}{2}$)和(2,+∞)上单调递减,在($\frac{1}{2}$,2)单调递增
故f(x)极大=f(2)=$\frac{5}{2}$ln2-$\frac{3}{2}$;
(2)f′(x)=-$\frac{(x-m)(x-\frac{1}{m})}{{x}^{2}}$,x>0,m>0)
①当0<m<1时,则$\frac{1}{m}$>1,故x∈(0,m),f′(x)<0;
x∈(m,1)时,f′(x)>0
此时f(x)在(0,m)上单调递减,在(m,1)单调递增;
②当m=1时,则$\frac{1}{m}$=1,故x∈(0,1),有f′(x)=-$\frac{{(x-1)}^{2}}{{x}^{2}}$<0恒成立,
此时f(x)在(0,1)上单调递减;
③当m>1时,则0<$\frac{1}{m}$<1,
故x∈(0,$\frac{1}{m}$)时,f′(x)<0;x∈($\frac{1}{m}$,1)时,f′(x)>0,
此时f(x)在(0,$\frac{1}{m}$)上单调递减,在($\frac{1}{m}$,1)单调递增.
点评 用导数,我们可解决曲线的切线问题,函数的单调性、极值与最值,正确求导是我们解题的关键.


 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:高中数学 来源: 题型:解答题
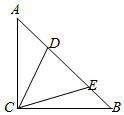 如图,等腰直角三角形区域ABC中,∠ACB=90°,BC=AC=1百米.现准备划出一块三角形区域CDE,其中D,E均在斜边AB上,且∠DCE=45°.记三角形CDE的面积为S.
如图,等腰直角三角形区域ABC中,∠ACB=90°,BC=AC=1百米.现准备划出一块三角形区域CDE,其中D,E均在斜边AB上,且∠DCE=45°.记三角形CDE的面积为S.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x≤-1} | B. | {x|-1≤x≤0} | C. | {x|0≤x≤1} | D. | {x|1≤x≤2} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,1-e2]∪[e2-1,+∞) | B. | [1-e2,e2-1] | ||
| C. | (-∞,e-2-1]∪[1-e-2,+∞) | D. | [e-2-1,1-e-2] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com