
【题目】如图,侧棱与底面垂直的四棱柱ABCD,A1B1C1D1的底面是梯形,AB∥CD,AB⊥AD,AA1=4,DC=2AB,AB=AD=3,点M在棱A1B1上,且A1M=![]() A1B1.已知点E是直线CD上的一点,AM∥平面BC1E.
A1B1.已知点E是直线CD上的一点,AM∥平面BC1E.
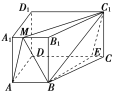
(1)试确定点E的位置,并说明理由;
(2)求三棱锥M-BC1E的体积.
科目:高中数学 来源: 题型:
【题目】我们把定义在![]() 上,且满足
上,且满足![]() (其中常数
(其中常数![]() 、
、![]() 满足
满足![]() ,
,![]() ,
,![]() )的函数叫做似周期函数.
)的函数叫做似周期函数.
(1)若某个似周期函数![]() 满足
满足![]() 且图象关于直线
且图象关于直线![]() 对称,求证:函数
对称,求证:函数![]() 是偶函数;
是偶函数;
(2)当![]() ,
,![]() 时,某个似周期函数在
时,某个似周期函数在![]() 时的解析式为
时的解析式为![]() ,求函数
,求函数![]() ,
,![]() ,
,![]() 的解析式;
的解析式;
(3)对于(2)中的函数![]() ,若对任意
,若对任意![]() ,都有
,都有![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 满足
满足![]() .
.
(1)证明:数列![]() 为等差数列;
为等差数列;
(2)设数列![]() 的前n项和为
的前n项和为![]() ,若
,若![]() ,且对任意的正整数n,都有
,且对任意的正整数n,都有![]() ,求整数
,求整数![]() 的值;
的值;
(3)设数列![]() 满足
满足![]() ,若
,若![]() ,且存在正整数s,t,使得
,且存在正整数s,t,使得![]() 是整数,求
是整数,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某烘焙店加工一个成本为60元的蛋糕,然后以每个120元的价格出售,如果当天卖不完,剩下的这种蛋糕作餐厨垃圾处理.
(1)若烘焙店一天加工16个这种蛋糕,,求当天的利润![]() (单位:元)关于当天需求量
(单位:元)关于当天需求量![]() (单位:个,
(单位:个,![]() )的函数解析式;
)的函数解析式;
(2)烘焙店记录了100天这种蛋糕的日需求量(单位:个),整理得下表:
日需求量 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
频数 | 10 | 20 | 16 | 16 | 15 | 13 | 10 |
①若烘焙店一天加工16个这种蛋糕,![]() 表示当天的利润(单位:元),求
表示当天的利润(单位:元),求![]() 的分布列与数学期望及方差;
的分布列与数学期望及方差;
②若烘焙店一天加工16个或17个这种蛋糕,仅从获得利润大的角度考虑,你认为应加工16个还是17个?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国古代计时器的发明时间不晚于战国时代(公元前476年~前222年),其中沙漏就是古代利用机械原理设计的一种计时装置,它由两个形状完全相同的容器和一个狭窄的连接管道组成,开始时细沙全部在上部容器中,细沙通过连接管道流到下部容器,如图,某沙漏由上、下两个圆锥容器组成,圆锥的底面圆的直径和高均为8 cm,细沙全部在上部时,其高度为圆锥高度的![]() (细管长度忽略不计).若细沙全部漏入下部后,恰好堆成一个盖住沙漏底部的圆锥形沙堆,则此圆锥形沙堆的高为( )
(细管长度忽略不计).若细沙全部漏入下部后,恰好堆成一个盖住沙漏底部的圆锥形沙堆,则此圆锥形沙堆的高为( )
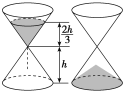
A.2 cmB.![]() cmC.
cmC.![]() cmD.
cmD.![]() cm
cm
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,有四座城市![]() 、
、![]() 、
、![]() 、
、![]() ,其中
,其中![]() 在
在![]() 的正东方向,且与
的正东方向,且与![]() 相距
相距![]() ,
,![]() 在
在![]() 的北偏东
的北偏东![]() 方向,且与
方向,且与![]() 相距
相距![]() ;
;![]() 在
在![]() 的北偏东
的北偏东![]() 方向,且与
方向,且与![]() 相距
相距![]() ,一架飞机从城市
,一架飞机从城市![]() 出发以
出发以![]() 的速度向城市
的速度向城市![]() 飞行,飞行了
飞行,飞行了![]() ,接到命令改变航向,飞向城市
,接到命令改变航向,飞向城市![]() ,此时飞机距离城市
,此时飞机距离城市![]() 有( )
有( )
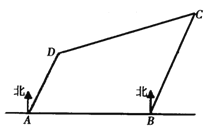
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com