练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    在数列{an}中,a1=2,3(a1+a2+…+an)=(n+2)an,n∈N*,则an=　　　　. 


    n(n+1)解析:由已知可得3Sn=(n+2)an,当n≥2时,

    3(Sn-Sn-1)=(n+2)an-(n+1)an-1=3an,

    ∴=.

    ∵a1···…··=2×××××…××=n(n+1),

    ∴an=n(n+1).


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    过抛物线y2＝2px(p>0)的焦点作倾斜角为30°的直线l与抛物线交于P，Q两点，分别过P，Q两点作PP1，QQ1垂直于抛物线的准线于P1，Q1，若|PQ|＝2，则四边形PP1Q1Q的面积是(　　)

    A．1  B．2  C．3  D.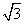

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    数列{an}满足a1=2,且对任意的m,n∈N*,都有=an,则a3=　　　　;{an}的前n项和Sn=　　　　. 

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    正项数列{an}满足-(2n-1)an-2n=0.

    (1)求数列{an}的通项公式an;

    (2)令bn=,求数列{bn}的前n项和Tn.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知数列{an}的通项公式是an=,那么这个数列是(　　)

    (A)递增数列 (B)递减数列

    (C)摆动数列 (D)常数列

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    .已知数列{an}的前n项和Sn与通项an满足Sn=-an.

    (1)求数列{an}的通项公式;

    (2)设f(x)=log3x,bn=f(a1)+f(a2)+…+f(an),Tn=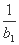++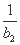…+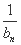,求T2012;

    (3)若cn=an·f(an),求{cn}的前n项和Un.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知f(x)是奇函数,g(x)是偶函数,且f(-1)+g(1)=2,f(1)+g(-1)=4,则g(1)等于(　　)

    (A)4    (B)3    (C)2    (D)1

    查看答案和解析>>

    科目：高中数学 来源： 题型：


     “函数g(x)=(2-a)在区间(0,+∞)上是增函数”的充分不必要条件是a∈　                   . 

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若a,b,c成等比数列,则函数f(x)=ax2+bx+c的图象与x轴交点的个数为　　　　. 

    查看答案和解析>>

    同步练习册答案