
.已知数列{an}的前n项和Sn与通项an满足Sn= -
- an.
an.
(1)求数列{an}的通项公式;
(2)设f(x)=log3x,bn=f(a1)+f(a2)+…+f(an),Tn=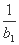 +
+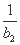 +…+
+…+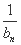 ,求T2012;
,求T2012;
(3)若cn=an·f(an),求{cn}的前n项和Un.
解:(1)当n=1时,a1=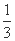 ,
,
当n≥2时,an=Sn-Sn-1= -
- an-
an- +
+ an-1,
an-1,
所以an=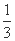 an-1,
an-1,
即数列{an}是首项为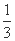 ,公比为
,公比为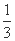 的等比数列,
的等比数列,
故an=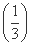 n.
n.
(2)由已知可得f(an)=log3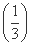 n=-n.
n=-n.
则bn=-1-2-3-…-n=- ,
,
故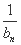 =-2(
=-2( -
- ),
),
又Tn=-2[(1- )+(
)+( -
-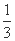 )+…+(
)+…+( -
- )]
)]
=-2(1- ),
),
所以T2012=-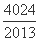 .
.
(3)由题意得cn=-n·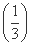 n,
n,
故Un=c1+c2+…+cn
=-[1×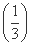 1+2×
1+2×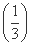 2+…+n×
2+…+n×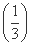 n],
n],
则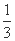 Un=-[1×
Un=-[1×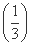 2+2×
2+2×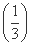 3+…+n×
3+…+n×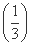 n+1],
n+1],
两式相减可得
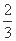 Un=-[
Un=-[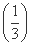 1+
1+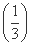 2+…+
2+…+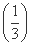 n-n·
n-n·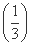 n+1]
n+1]
=- [1-
[1-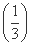 n]+n·
n]+n·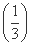 n+1
n+1
=- +
+ ·
·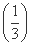 n+n·
n+n·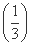 n+1,
n+1,
则Un=- +
+ ·
·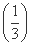 n+
n+ n·
n·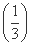 n+1.
n+1.


科目:高中数学 来源: 题型:
已知抛物线C的顶点在坐标原点,焦点为F(0,-1),直线l与抛物线C相交于A,B两点,若AB的中点为(2,-2),则直线l的方程为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知数列{an}的前n项和为Sn,且Sn=2n2+n,n∈N*,数列{bn}满足an=4log2bn+3,n∈N*.
(1)求an,bn;
(2)求数列{an·bn}的前n项和Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:
设f(x)为定义在R上的奇函数.当x≥0时,f(x)=2x+2x+b(b为常数),则f(-1)等于( )
(A)-3 (B)-1 (C)1 (D)3
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数f(x)=2mx2-2(4-m)x+1,g(x)=mx,若对于任一实数x,f(x)与g(x)至少有一个为正数,则实数m的取值范围是( )
(A)(0,2) (B)(0,8) (C)(2,8) (D)(-∞,0)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com