
分析 由题意画出图形,数形结合可得使A∩B=∅的实数a的取值范围.
解答 解:A={(x,y)||x|≤1,|y|≤1},B={(x,y)|(x-a)2+(y-a)2<1},
如图,|ON|=$\sqrt{2}$+1,则|OM|=1+$\frac{\sqrt{2}}{2}$,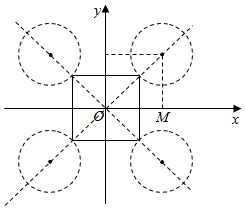
要使A∩B=∅,则a≥1+$\frac{\sqrt{2}}{2}$或a≤-1-$\frac{\sqrt{2}}{2}$.
故答案为:(-∞,-1-$\frac{\sqrt{2}}{2}$]]∪[1+$\frac{\sqrt{2}}{2}$,+∞).
点评 本题主要考查二元一次不等式(组)与平面区域、集合关系中的参数取值问题、不等式的解法等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 充分条件而非必要条件 | B. | 必要条件而非充分条件 | ||
| C. | 充要条件 | D. | 非充分条件也非必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4a-2m | B. | 4a | C. | 4a+m | D. | 4a+2m |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
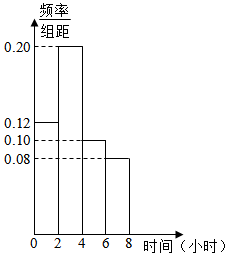 研究人员随机调查统计了某地1000名“上班族”每天在工作之余使用手机上网的时间,并将其绘制为如图所示的频率分布直方图.若同一组数据用该区间的中点值作代表,则可估计该地“上班族”每天在工作之余使用手机上网的平均时间是( )
研究人员随机调查统计了某地1000名“上班族”每天在工作之余使用手机上网的时间,并将其绘制为如图所示的频率分布直方图.若同一组数据用该区间的中点值作代表,则可估计该地“上班族”每天在工作之余使用手机上网的平均时间是( )| A. | 1.78小时 | B. | 2.24小时 | C. | 3.56小时 | D. | 4.32小时 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com