
| 喜欢看足球比赛 | 不喜欢看足球比赛 | 总计 | |
| 男 | |||
| 女 | |||
| 总计 |
| P(K2≥k0) | 0.4 | 0.25 | 0.10 | 0.010 |
| k0 | 0.708 | 1.323 | 2.706 | 6.635 |
分析 (1)本题是一个简单的数字的运算,根据a,b,c,d的已知和未知的结果,做出空格处的结果.
(2)由已知数据可求得观测值,把求得的观测值同临界值进行比较,得到在犯错的概率不超过0.10的前提下不能判断性别与喜欢看足球比赛有关.
(3)求出基本事件的个数,即可求出恰有一男一女播音的概率.
解答 解:(1)2×2列联表:
| 喜欢看足球比赛 | 不喜欢看足球比赛 | 总计 | |
| 男 | 8 | 4 | 12 |
| 女 | 4 | 6 | 10 |
| 总计 | 12 | 10 | 22 |
点评 本题考查独立性检验的列联表.考查假设性判断,考查古典概型概率的计算,是一个综合题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
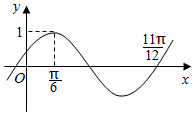 函数f(x)=Asin(ωx+φ)(A>0,ω>0)的图象如图所示,则以下步骤可以得到函数f(x)的图象的是( )
函数f(x)=Asin(ωx+φ)(A>0,ω>0)的图象如图所示,则以下步骤可以得到函数f(x)的图象的是( )| A. | 将y=sinx的图象上的点纵坐标不变,横坐标变成原来的2倍,然后再向左平移$\frac{π}{6}$个单位 | |
| B. | 将y=sinx的图象上的点纵坐标不变,横坐标变成原来的2倍,然后再向右平移$\frac{π}{6}$个单位 | |
| C. | 将y=sinx的图象上的点纵坐标不变,横坐标变成原来的$\frac{1}{2}$,然后再向右平移$\frac{π}{12}$个单位 | |
| D. | 将y=sinx的图象上的点纵坐标不变,横坐标变成原来的$\frac{1}{2}$,然后再向左平移$\frac{π}{12}$个单位 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{9}$ | B. | $\frac{1}{3}$ | C. | $\frac{4}{9}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 大前提错误 | B. | 小前提错误 | ||
| C. | 推理形式错误 | D. | 大前提与推理形式都错误 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
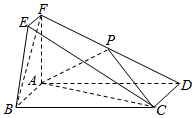 在如图所示的几何体中,四边形ABCD为矩形,平面ABEF⊥平面ABCD,EF∥AB,∠BAF=90°,AD=2,AB=AF=2FE=1,点P在棱DF上.
在如图所示的几何体中,四边形ABCD为矩形,平面ABEF⊥平面ABCD,EF∥AB,∠BAF=90°,AD=2,AB=AF=2FE=1,点P在棱DF上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com