
���� ����ͨ��|OA|=|OF|=$\sqrt{2}$�ɵ�b��c��ֵ�������ɵý��ۣ�
����ͨ����1��֪C��-2��0����D��2��0������ֱ��CM���̲�����Բ����������Τ�ﶨ���ɵõ�P���꣬����$\overrightarrow{QM}•\overrightarrow{DP}$=0�����㼴�ý��ۣ�
��� �⣺����|OA|=|OF|=$\sqrt{2}$����$b=c=\sqrt{2}$��
��a2=b2+c2=4��
����Բ����Ϊ��$\frac{x^2}{4}+\frac{y^2}{2}=1$��
�����ۣ�����Q��0��0����ʹ����MPΪֱ����Բ���ֱ��DP��MQ�Ľ��㣮
�������£�
�ɣ�1��֪��C��-2��0����D��2��0����
���������CM��y=k��x+2����P��x1��y1����
��MD��CD����M��2��4k����
����$\left\{\begin{array}{l}\frac{x^2}{4}+\frac{y^2}{2}=1\;\\ y=k��x+2��\end{array}\right.$����ȥy�������ã���1+2k2��x2+8k2x+8k2-4=0��
���=��8k2��2-4��1+2k2����8k2-4����0��
��$-2{x_1}=\frac{{8{k^2}-4}}{{1+2{k^2}}}����{x_1}=\frac{{2-4{k^2}}}{{1+2{k^2}}}$��
��${y_1}=k��{x_1}+2��=\frac{4k}{{1+2{k^2}}}$��
��$��P��\frac{{2-4{k^2}}}{{1+2{k^2}}}��\frac{{4{k^{\;}}}}{{1+2{k^2}}}��$��
��Q��x0��0������x0��-2��
����MPΪֱ����Բ����DP��MQ�Ľ��㣬
��MQ��DP����$\overrightarrow{QM}•\overrightarrow{DP}$=0�������
��$\overrightarrow{QM}=��2-{x_0}��4k��$��$\overrightarrow{DP}=��\frac{{-8{k^2}}}{{1+2{k^2}}}��\frac{4k}{{1+2{k^2}}}��$��
��$\overrightarrow{QM}•\overrightarrow{DP}=��2-{x_0}��•\frac{{-8{k^2}}}{{1+2{k^2}}}+4k•\frac{4k}{{1+2{k^2}}}=0$��
��$\frac{{8{k^2}}}{{1+2{k^2}}}{x_0}=0$���������x0=0��
�����Q��0��0����ʹ����MPΪֱ����Բ���ֱ��DP��MQ�Ľ��㣮
���� ������һ��ֱ����Բ���ߵ��ۺ��⣬��������Բ���̣������������������ע����ⷽ���Ļ��ۣ��������⣮


 ������ѧ���̲���ȫ���ϵ�д�
������ѧ���̲���ȫ���ϵ�д� ������ʱ����ҵ����ϵ�д�
������ʱ����ҵ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | 2 | C�� | 4 | D�� | $\frac{1}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ijУ�ƻ���һ��յ��Ͻ���һ�����Ϊ1800m2�ľ�����Ӿ�أ���ͼ��ʾ�����������߶����п�6m����Ϣ̨�������͵ײ������п�Ϊ3m�����е��������ƿյصij������ʹ���ÿյص������С��
ijУ�ƻ���һ��յ��Ͻ���һ�����Ϊ1800m2�ľ�����Ӿ�أ���ͼ��ʾ�����������߶����п�6m����Ϣ̨�������͵ײ������п�Ϊ3m�����е��������ƿյصij������ʹ���ÿյص������С���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� |  | B�� | 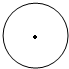 | C�� | 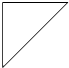 | D�� |  |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | {��1��-2��} | B�� | {��1��2��} | C�� | ��1��2�� | D�� | ��1��-2�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ��һ����ת��ɳ©���ϲ�Ϊһ����Բ̨���²�ΪһԲ�����ٶ���
��ͼ��һ����ת��ɳ©���ϲ�Ϊһ����Բ̨���²�ΪһԲ�����ٶ���| A�� |  | B�� |  | C�� |  | D�� |  |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com