
分析 根据奇偶性的定义与单调性的定义,即可证明函数y=$\frac{{2}^{x}-1}{{2}^{x}+1}$是定义域R上的奇函数,且为单调增函数.
解答 证明:函数y=f(x)=$\frac{{2}^{x}-1}{{2}^{x}+1}$的定义域为R,
任取x∈R,都有f(-x)=$\frac{{2}^{-x}-1}{{2}^{-x}+1}$=$\frac{1{-2}^{x}}{1{+2}^{x}}$=-$\frac{{2}^{x}-1}{{2}^{x}+1}$=-f(x),
∴f(x)是定义域R上的奇函数;
又任取x1、x2∈R,且x1<x2,
则f(x1)-f(x2)=$\frac{{2}^{{x}_{1}}-1}{{2}^{{x}_{1}}+1}$-$\frac{{2}^{{x}_{2}}-1}{{2}^{{x}_{2}}+1}$=$\frac{2{(2}^{{x}_{1}}{-2}^{{x}_{2}})}{{(2}^{{x}_{1}}+1){(2}^{{x}_{2}}+1)}$,
∵x1<x2,∴${2}^{{x}_{1}}$<${2}^{{x}_{2}}$,∴2(${2}^{{x}_{1}}$-${2}^{{x}_{2}}$)<0,且${2}^{{x}_{1}}$+1>0,${2}^{{x}_{2}}$+1>0,
∴f(x1)-f(x2)<0,即f(x1)<f(x2),
∴f(x)在定义域R上是单调增函数.
点评 本题考查了函数的奇偶性与单调性的定义与应用问题,是基础题目.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{5π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{3}$(4n-1) | B. | $\frac{16}{3}$(4n-1) | C. | $\frac{16}{3}$(2n-1) | D. | $\frac{4}{3}$(2n-1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(m+1)≥0 | B. | f(m+1)≤0 | C. | f(m+1)>0 | D. | f(m+1)<0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 设P是正六边形OABCDE的中心,若$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,试用向量$\overrightarrow{a}$,$\overrightarrow{b}$表示$\overrightarrow{PB}$、$\overrightarrow{OC}$、$\overrightarrow{OD}$.
设P是正六边形OABCDE的中心,若$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,试用向量$\overrightarrow{a}$,$\overrightarrow{b}$表示$\overrightarrow{PB}$、$\overrightarrow{OC}$、$\overrightarrow{OD}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
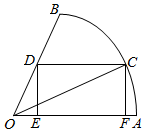 圆心角为60°的扇形AOB的半径为1,C是AB弧上一点,作矩形CDEF,如图,当C点在什么位置时,这个矩形的面积最大?这时的;∠AOC等于多少度?
圆心角为60°的扇形AOB的半径为1,C是AB弧上一点,作矩形CDEF,如图,当C点在什么位置时,这个矩形的面积最大?这时的;∠AOC等于多少度?查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com