
| A. | a>b>c | B. | b>c>a | C. | b>a>c | D. | a>c>b |
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:高中数学 来源: 题型:解答题
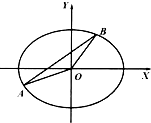 已知椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$,不经过原点O的直线l:y=kx+m(k>0)与椭圆E相交于不同的两点A、B,直线OA,AB,OB的斜率依次构成等比数列.
已知椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$,不经过原点O的直线l:y=kx+m(k>0)与椭圆E相交于不同的两点A、B,直线OA,AB,OB的斜率依次构成等比数列.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在三棱柱ABC-A1B1C1中,G为ABC的重心,延长线段AG交BC于F,B1F交BC1于E.
如图,在三棱柱ABC-A1B1C1中,G为ABC的重心,延长线段AG交BC于F,B1F交BC1于E.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
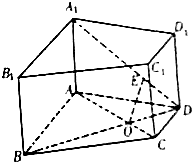 如图,在四棱柱ABCD-A1B1C1D1中,AB∥CD,AB⊥AD,AB=4,AD=2$\sqrt{2}$,CD=2,AA1=2,侧棱AA1⊥底面ABCD,E是A1D上一点,且A1E=2ED.
如图,在四棱柱ABCD-A1B1C1D1中,AB∥CD,AB⊥AD,AB=4,AD=2$\sqrt{2}$,CD=2,AA1=2,侧棱AA1⊥底面ABCD,E是A1D上一点,且A1E=2ED.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,AB为圆O的直径,PA垂直圆O所在的平面,点C为圆O上的一点.
如图,AB为圆O的直径,PA垂直圆O所在的平面,点C为圆O上的一点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
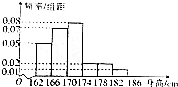 2016年高考报名体检中,某市共有40000名男生参加体检,体检其中一项为测量身高,统计调查数据显示所有男生的身高服从正态分布N(170,16).统计人员从市一中高三的参加体检的男生中随机抽取了50名进行身高测量,所得数据全部介于162cm和186cm之间,并将测量数据分成6组:第一组[162,166),第二组[166,170),…,第六组[182,186),然后按上述分组方式绘制得到如图所示的频率分布直方图.
2016年高考报名体检中,某市共有40000名男生参加体检,体检其中一项为测量身高,统计调查数据显示所有男生的身高服从正态分布N(170,16).统计人员从市一中高三的参加体检的男生中随机抽取了50名进行身高测量,所得数据全部介于162cm和186cm之间,并将测量数据分成6组:第一组[162,166),第二组[166,170),…,第六组[182,186),然后按上述分组方式绘制得到如图所示的频率分布直方图.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com