
分析 首先利用定积分求出阴影部分区域面积,然后利用定积分求几何概型概率.
解答 解:如图,区域Ω对应的部分是边长为1的正方形,区域A对应部分为图中阴影部分,面积为${∫}_{0}^{1}\sqrt{x}dx=\frac{2}{3}{x}^{\frac{3}{2}}{|}_{0}^{1}=\frac{2}{3}$,
由几何概型公式得到在区域Ω中随机取一个点,则该点在A中的概率为$\frac{\frac{2}{3}}{1}$=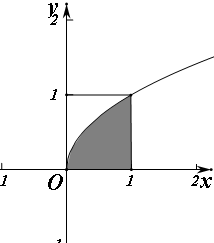 $\frac{2}{3}$;
$\frac{2}{3}$;
故答案为:$\frac{2}{3}$.
点评 本题考查了定积分求曲边梯形的面积以及几何概型的求法;利用面积比求概率是几何概型的概率求法中经常运用的方法.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>b>c | B. | b>c>a | C. | b>a>c | D. | a>c>b |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知ABCD是边长为2的正方形,EA⊥平面ABCD,FC∥EA,设EA=1,FC=2.
如图,已知ABCD是边长为2的正方形,EA⊥平面ABCD,FC∥EA,设EA=1,FC=2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 17 | B. | 23 | C. | 34 | D. | 46 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①③ | B. | ①② | C. | ①③④ | D. | ②③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com