练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    11．${（x+\frac{1}{x}-2）^5}$展开式中常数项为（　　）
    A．160B．-160C．252D．-252

    分析 ${（x+\frac{1}{x}-2）^5}={（\sqrt{x}-\frac{1}{{\sqrt{x}}}）^{10}}$．展开式通项公式${T_{r+1}}=C_{10}^r{x^{\frac{1}{2}（10-r）}}{（-1）^r}{x^{-\frac{1}{2}r}}={（-1）^r}C_{10}^r{x^{5-r}}$，令5-r=0，解出r即可得出．

    解答 解：${（x+\frac{1}{x}-2）^5}={（\sqrt{x}-\frac{1}{{\sqrt{x}}}）^{10}}$．
     展开式通项公式${T_{r+1}}=C_{10}^r{x^{\frac{1}{2}（10-r）}}{（-1）^r}{x^{-\frac{1}{2}r}}={（-1）^r}C_{10}^r{x^{5-r}}$，
    当且仅当r=5时，T6=-${∁}_{10}^{5}$=-252 为常数项．
    故选：D．

    点评 本题考查了二项式定理的应用，考查了推理能力与计算能力，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    1．袋中装有5只大小相同的球，编号分别为1，2，3，4，5，现从该袋中随机地取出3只，被取出的球
    中最大的号码为ξ，则Eξ=$\frac{9}{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

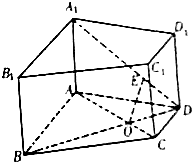    2．如图，在四棱柱ABCD-A1B1C1D1中，AB∥CD，AB⊥AD，AB=4，AD=2$\sqrt{2}$，CD=2，AA1=2，侧棱AA1⊥底面ABCD，E是A1D上一点，且A1E=2ED．
    （1）求证：EO∥平面A1ABB1；
    （2）求直线A1B与平面A1ACC1所成角的正弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    19．设区域Ω={（x，y）|0≤x≤1，0≤y≤1}，区域A={（x，y）|y≤$\sqrt{x}$，（x，y）∈Ω}，在区域Ω中随机取一个点，则该点在A中的概率$\frac{2}{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    6．中位数为2016的一组数构成等差数列，其末项为（1+x）4028的展开式倒数第二项的系数，则该数列的首项为4．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    16．已知$\overrightarrow{a}$=（1，1），$\overrightarrow{b}$=（-2，-2），|$\overrightarrow{c}$|=2$\sqrt{2}$，$\overrightarrow{c}$•（$\overrightarrow{a}$+$\overrightarrow{b}$）=2，则$\overrightarrow{a}$和$\overrightarrow{c}$的夹角θ=120°．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．实数x，y满足$\left\{\begin{array}{l}{x+y-a≤0}\\{x-y≥0}\\{y≥0}\\{\;}\end{array}\right.$，若z=x-2y的最小值为-1，则实数a的值为（　　）
    A．2B．1C．0D．-1

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    20．在平面直角坐标系中，“点M的坐标满足方程4$\sqrt{x}$+y=0”是“点M在曲线y2=16x上”的（　　）
    A．充分非必要条件B．必要非充分条件
    C．充要条件D．既非充分也非必要条件

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    1．已知向量$\overrightarrow{a}$=（cosα，sinα），$\overrightarrow{b}$=（cosβ，sinβ），且$\overrightarrow{a}$，$\overrightarrow{b}$满足关系|k$\overrightarrow{a}$+$\overrightarrow{b}$|=$\sqrt{3}$|$\overrightarrow{a}$-k$\overrightarrow{b}$|（k为正数）．
    （1）求$\overrightarrow{a}$与$\overrightarrow{b}$的数量积用k表示的解析式f（k）．
    （2）$\overrightarrow{a}$能否与$\overrightarrow{b}$垂直？$\overrightarrow{a}$能否与$\overrightarrow{b}$平行？若不能，说明理由；若能，求出相应的k值．

    查看答案和解析>>

    同步练习册答案