
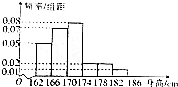
 2016年高考报名体检中,某市共有40000名男生参加体检,体检其中一项为测量身高,统计调查数据显示所有男生的身高服从正态分布N(170,16).统计人员从市一中高三的参加体检的男生中随机抽取了50名进行身高测量,所得数据全部介于162cm和186cm之间,并将测量数据分成6组:第一组[162,166),第二组[166,170),…,第六组[182,186),然后按上述分组方式绘制得到如图所示的频率分布直方图.
2016年高考报名体检中,某市共有40000名男生参加体检,体检其中一项为测量身高,统计调查数据显示所有男生的身高服从正态分布N(170,16).统计人员从市一中高三的参加体检的男生中随机抽取了50名进行身高测量,所得数据全部介于162cm和186cm之间,并将测量数据分成6组:第一组[162,166),第二组[166,170),…,第六组[182,186),然后按上述分组方式绘制得到如图所示的频率分布直方图.分析 高三男生的平均身高用组中值×频率,即可得到结论;
先根据正态分布的规律求出全市前52名的身高在182cm以上的50人中的人数,确定X的可能取值,求出其概率,即可得到X的分布列与期望.
解答 解:由直方图,经过计算该校高三年级男生平均身高为:
164×0.05×4+168×0.07×4+17×0.08×4+176×0.02×4+18×0.02×4+184×0.01×4=170.72,
高于全市平均身高170,
(2)由男生身高在178cm以上(含178cm)的人中总共有0.12×5=6人,
∵P(170-3×4<X≤170+3×4)=0.9974.
∴P(X≥182)=$\frac{1-0.9974}{2}$=0.0013,
全省高中男生身高排名(从高到低) 前52名中最低身高是182 cm;
全省前52名的身高在182cm以上,这50人中182cm以上的有2人.
随机变量X可取0,1,2,于是:
P(X=0)=$\frac{{C}_{4}^{3}}{{C}_{6}^{3}}$=0.2,
P(X=1)=$\frac{{C}_{4}^{2}{C}_{2}^{1}}{{C}_{6}^{3}}$=0.6,
P(X=2)=$\frac{{C}_{4}^{1}•{C}_{2}^{2}}{{C}_{6}^{3}}$=0.2;
E(X)=0×0.2+1×0.6+2×0.2=1.
点评 此题主要考查了正态分布,考查随机变量的定义及其分布列,并考查了利用分布列求其期望.正确理解频数分布直方图横纵轴表示的意义,由频数分布直方图可以得到什么结论是学习中需要掌握的关键.


 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | a>b>c | B. | b>c>a | C. | b>a>c | D. | a>c>b |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①③ | B. | ①② | C. | ①③④ | D. | ②③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 9•10n-1 | B. | $\left\{{\begin{array}{l}{11}\\{9•{{10}^{n-1}}}\end{array}\begin{array}{l}{,n=1}\\{,n≥2}\end{array}}\right.$ | ||
| C. | 10n+1 | D. | $\left\{{\begin{array}{l}9\\{{{10}^n}+1}\end{array}\begin{array}{l}{,n=1}\\{,n≥2}\end{array}}\right.$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {a1|a1≥2016,a1∈N*} | B. | {a1|a1≥2015,a1∈N*} | C. | {a1|a1≥2014,a1∈N*} | D. | {a1|a1≥2013,a1∈N*} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com