
ЗжЮі РћгУЁАЕШЗНВюЪ§СаЁБгыЁАЕШВюЪ§СаЁБЕФЖЈвхМАЦфаджЪМДПЩХаЖЯГіНсТлЃЎ
НтД№ НтЃКЂй{an}ЪЧЁАЕШЗНВюЪ§СаЁБЃЌЁрa${\;}_{n}^{2}$-a${\;}_{n-1}^{2}$=pЃЈnЁн2ЃЌnЁЪN*ЃЌpЮЊГЃЪ§ЃЉЃЌдђЪ§Са{an2}ЪЧЕШВюЪ§СаЃЌе§ШЗЃЛ
ЂкЁпan=ЃЈ-1ЃЉnЃЌЁр${a}_{n}^{2}$=1ЃЌдђnЁн2ЪБЃЌa${\;}_{n}^{2}$-a${\;}_{n-1}^{2}$ЃЌ=0ЃЌЁрЪ§Са{an}ЮЊЕШЗНВюЪ§СаЃЌе§ШЗЃЛ
Ђл{an}ЪЧЁАЕШЗНВюЪ§СаЁБЃЌдђЪ§Са{akn}ЃЈkЁЪN*ЃЌkЮЊГЃЪ§ЃЉПЩФмЛЙЪЧЁАЕШЗНВюЪ§СаЁБЃЌШЁan=2ТњзуЬѕМўЃЌвђДЫВЛе§ШЗЃЛ
ЂмШє{an}МШЪЧЁАЕШЗНВюЪ§СаЁБЃЌгжЪЧЕШВюЪ§СаЃЌЩшЙЋВюЮЊdЃЌЁрnЁн2ЪБЃЌa${\;}_{n}^{2}$-a${\;}_{n-1}^{2}$=$[{a}_{1}+ЃЈn-1ЃЉd]^{2}$$-[{a}_{1}+ЃЈn-2ЃЉd]^{2}$=d[2a1+ЃЈ2n-3ЃЉd]ЮЊГЃЪ§ЃЌБиШЛd=0ЃЌ
дђИУЪ§СаЪЧГЃЪ§СаЃЌе§ШЗЃЎ
ЙЪД№АИЮЊЃКЂйЂкЂмЃЎ
ЕуЦР БОЬтПМВщСЫЕШВюЪ§СаЕФЭЈЯюЙЋЪНМАЦфаджЪЁЂаТЖЈвхЁЂЁАЕШЗНВюЪ§СаЁБЃЌПМВщСЫЭЦРэФмСІгыМЦЫуФмСІЃЌЪєгкжаЕЕЬтЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
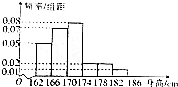 2016ФъИпПМБЈУћЬхМьжаЃЌФГЪаЙВга40000УћФаЩњВЮМгЬхМьЃЌЬхМьЦфжавЛЯюЮЊВтСПЩэИпЃЌЭГМЦЕїВщЪ§ОнЯдЪОЫљгаФаЩњЕФЩэИпЗўДге§ЬЌЗжВМNЃЈ170ЃЌ16ЃЉЃЎЭГМЦШЫдБДгЪавЛжаИпШ§ЕФВЮМгЬхМьЕФФаЩњжаЫцЛњГщШЁСЫ50УћНјааЩэИпВтСПЃЌЫљЕУЪ§ОнШЋВПНщгк162cmКЭ186cmжЎМфЃЌВЂНЋВтСПЪ§ОнЗжГЩ6зщЃКЕквЛзщ[162ЃЌ166ЃЉЃЌЕкЖўзщ[166ЃЌ170ЃЉЃЌЁЃЌЕкСљзщ[182ЃЌ186ЃЉЃЌШЛКѓАДЩЯЪіЗжзщЗНЪНЛцжЦЕУЕНШчЭМЫљЪОЕФЦЕТЪЗжВМжБЗНЭМЃЎ
2016ФъИпПМБЈУћЬхМьжаЃЌФГЪаЙВга40000УћФаЩњВЮМгЬхМьЃЌЬхМьЦфжавЛЯюЮЊВтСПЩэИпЃЌЭГМЦЕїВщЪ§ОнЯдЪОЫљгаФаЩњЕФЩэИпЗўДге§ЬЌЗжВМNЃЈ170ЃЌ16ЃЉЃЎЭГМЦШЫдБДгЪавЛжаИпШ§ЕФВЮМгЬхМьЕФФаЩњжаЫцЛњГщШЁСЫ50УћНјааЩэИпВтСПЃЌЫљЕУЪ§ОнШЋВПНщгк162cmКЭ186cmжЎМфЃЌВЂНЋВтСПЪ§ОнЗжГЩ6зщЃКЕквЛзщ[162ЃЌ166ЃЉЃЌЕкЖўзщ[166ЃЌ170ЃЉЃЌЁЃЌЕкСљзщ[182ЃЌ186ЃЉЃЌШЛКѓАДЩЯЪіЗжзщЗНЪНЛцжЦЕУЕНШчЭМЫљЪОЕФЦЕТЪЗжВМжБЗНЭМЃЎВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
| AЃЎ | ГЄЖШЯрЕШЕФЯђСПНаЯрЕШЯђСП | |
| BЃЎ | СуЯђСПЕФГЄЖШЮЊСу | |
| CЃЎ | ЙВЯпЯђСПЪЧдквЛЬѕжБЯпЩЯЕФЯђСП | |
| DЃЎ | ЦНааЯђСПОЭЪЧЯђСПЫљдкЕФжБЯпЦНааЕФЯђСП |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
| AЃЎ | $\frac{\sqrt{6}-\sqrt{2}}{2}$ | BЃЎ | $\frac{\sqrt{6}+\sqrt{2}}{2}$ | CЃЎ | $\frac{2+\sqrt{3}}{4}$ | DЃЎ | $\frac{2-\sqrt{3}}{4}$ |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
| AЃЎ | fЃЈsinxЃЉЃОfЃЈcosxЃЉ | BЃЎ | fЃЈ$\frac{{x}^{2}+1}{2}$ЃЉЃОfЃЈxЃЉ | ||
| CЃЎ | fЃЈ$\frac{1}{{3}^{x}+1}$ЃЉЁнfЃЈ$\frac{1}{{2}^{x}+1}$ЃЉ | DЃЎ | fЃЈ$\frac{1}{{3}^{x}+{3}^{-x}}$ЃЉЁнfЃЈ$\frac{1}{{2}^{x}+{2}^{-x}}$ЃЉ |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
 ШчЭМЫљЪОЃЌAFЁЂDEЗжБ№ЪЧЁбOЁЂЁбO1ЕФжБОЖЃЌADгыСНдВЫљдкЕФЦНУцОљДЙжБЃЌAD=8ЃЌBCЪЧЁбOЕФжБОЖЃЌAB=AC=6ЃЌOEЁЮADЃЎ
ШчЭМЫљЪОЃЌAFЁЂDEЗжБ№ЪЧЁбOЁЂЁбO1ЕФжБОЖЃЌADгыСНдВЫљдкЕФЦНУцОљДЙжБЃЌAD=8ЃЌBCЪЧЁбOЕФжБОЖЃЌAB=AC=6ЃЌOEЁЮADЃЎВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com