
| A. | {a1|a1≥2016,a1∈N*} | B. | {a1|a1≥2015,a1∈N*} | C. | {a1|a1≥2014,a1∈N*} | D. | {a1|a1≥2013,a1∈N*} |
分析 化简构造可得{(an-1)2}是以(a1-1)2为首项,以1为公差的等差数列,从而可得(an-1)2=(a1-1)2+n-1,从而代入求解即可.
解答 解:∵an+1=$\sqrt{{a}_{n}^{2}-2{a}_{n}+2}$+1,
∴an+1-1=$\sqrt{{a}_{n}^{2}-2{a}_{n}+2}$,
∴(an+1-1)2=(an-1)2+1,
∴{(an-1)2}是以(a1-1)2为首项,以1为公差的等差数列,
∴(an-1)2=(a1-1)2+n-1,
∴(a2016-1)2=(a1-1)2+2015,
∴(a1-1)2=(a2016-1)2-2015>2015×2014,
又∵a1为正整数,
∴a1-1>$\sqrt{2015×2014}$,
∴a1≥2016,
故选A.
点评 本题考查了数列的性质的判断及整体思想与转化思想的应用,同时考查了构造法的应用.


科目:高中数学 来源: 题型:解答题
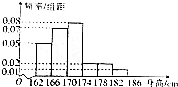 2016年高考报名体检中,某市共有40000名男生参加体检,体检其中一项为测量身高,统计调查数据显示所有男生的身高服从正态分布N(170,16).统计人员从市一中高三的参加体检的男生中随机抽取了50名进行身高测量,所得数据全部介于162cm和186cm之间,并将测量数据分成6组:第一组[162,166),第二组[166,170),…,第六组[182,186),然后按上述分组方式绘制得到如图所示的频率分布直方图.
2016年高考报名体检中,某市共有40000名男生参加体检,体检其中一项为测量身高,统计调查数据显示所有男生的身高服从正态分布N(170,16).统计人员从市一中高三的参加体检的男生中随机抽取了50名进行身高测量,所得数据全部介于162cm和186cm之间,并将测量数据分成6组:第一组[162,166),第二组[166,170),…,第六组[182,186),然后按上述分组方式绘制得到如图所示的频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(sinx)>f(cosx) | B. | f($\frac{{x}^{2}+1}{2}$)>f(x) | ||
| C. | f($\frac{1}{{3}^{x}+1}$)≥f($\frac{1}{{2}^{x}+1}$) | D. | f($\frac{1}{{3}^{x}+{3}^{-x}}$)≥f($\frac{1}{{2}^{x}+{2}^{-x}}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,AF、DE分别是⊙O、⊙O1的直径,AD与两圆所在的平面均垂直,AD=8,BC是⊙O的直径,AB=AC=6,OE∥AD.
如图所示,AF、DE分别是⊙O、⊙O1的直径,AD与两圆所在的平面均垂直,AD=8,BC是⊙O的直径,AB=AC=6,OE∥AD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
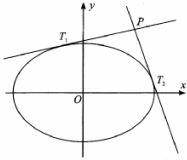 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1的短轴长为2,离心率$\frac{\sqrt{2}}{2}$.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1的短轴长为2,离心率$\frac{\sqrt{2}}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com