
分析 (1)利用互化公式即可把曲线C的极坐标方程ρ2-6ρcosθ+5=0化为直角坐标方程.直线l的参数方程为$\left\{\begin{array}{l}{x=7+tcosα}\\{y=tsinα}\end{array}\right.$(t为参数),代入曲线C的直角坐标方程可得t2+8tcosα+12=0,根据直线l与曲线C有公共点,可得△≥0,利用三角函数的单调性即可得出.
(2)曲线C的方程x2+y2-6x+5=0可化为(x-3)2+y2=4,其参数方程为$\left\{\begin{array}{l}{x=3+2cosθ}\\{y=2sinθ}\end{array}\right.$,(θ为参数),设M(x,y)为曲线上任意一点,可得2x+$\frac{3}{2}$y=6+4cosθ+3sinθ,利用和差公式化简即可得出取值范围.
解答 解:(1)将曲线C的极坐标方程ρ2-6ρcosθ+5=0化为直角坐标方程为x2+y2-6x+5=0,
直线l的参数方程为$\left\{\begin{array}{l}{x=7+tcosα}\\{y=tsinα}\end{array}\right.$(t为参数),
将参数方程代入x2+y2-6x+5=0,整理得t2+8tcosα+12=0,
∵直线l与曲线C有公共点,∴△=64cos2α-48≥0,
∴cosα≥$\frac{\sqrt{3}}{2}$,或cosα$≤-\frac{\sqrt{3}}{2}$,∵α∈[0,π),
∴α的取值范围是$[0,\frac{π}{6}]$∪$[\frac{5π}{6},π)$.
(2)曲线C的方程x2+y2-6x+5=0可化为(x-3)2+y2=4,
其参数方程为$\left\{\begin{array}{l}{x=3+2cosθ}\\{y=2sinθ}\end{array}\right.$,(θ为参数),
∵M(x,y)为曲线上任意一点,
∴$2x+\frac{3}{2}y=6+4cosθ+3sinθ=6+5sin({θ+φ})(sinφ=\frac{4}{5},cosφ=\frac{3}{5})$,
∴$2x+\frac{3}{2}y$的取值范围是[1,11].
点评 本题考查了极坐标方程化为直角坐标方程、参数方程的应用、三角函数求值,考查了推理能力与计算能力,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
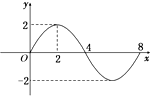 函数y=Asin(ωx+φ)(A>0,ω>0)的部分图象如图所示,则f(1)+f(2)+f(3)+…+f(2 012)的值等于( )
函数y=Asin(ωx+φ)(A>0,ω>0)的部分图象如图所示,则f(1)+f(2)+f(3)+…+f(2 012)的值等于( )| A. | $\sqrt{2}$ | B. | 2+2$\sqrt{2}$ | C. | $\sqrt{2}$+2 | D. | $\sqrt{2}$-2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{3\sqrt{3}}}{4}$ | B. | $\frac{{\sqrt{3}}}{4}$ | C. | $\frac{{3\sqrt{3}}}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
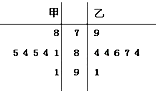 甲、乙两名运动员为了争取得到2016年巴西奥运会的最后一个参赛名额,共进行了7轮比赛,得分情况如茎叶图所示.
甲、乙两名运动员为了争取得到2016年巴西奥运会的最后一个参赛名额,共进行了7轮比赛,得分情况如茎叶图所示.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{25}$ | B. | $\frac{2}{19}$ | C. | $\frac{2}{13}$ | D. | $\frac{2}{7}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com