
| A. | p | B. | $\frac{4}{3}p$ | C. | 2p | D. | $\frac{8}{3}p$ |
分析 设抛物线y2=2px(p>0)的准线为l′:x=-$\frac{p}{2}$.如图所示,当直线AB的倾斜角为锐角时,分别过点A,B作AM⊥l′,BN⊥l′,垂足为M,N.过点B作BC⊥AM交于点C.则|AM|=|AF|,|BN|=|BF|.由于|AF|=3|BF|=$\frac{3}{4}$|AB|,可得|AM|-|BN|=|AC|=|AF|-|BF|=$\frac{1}{2}$|AB|,在Rt△ABC中,由|AC|=$\frac{1}{2}$|AB|,可得∠BAC=60°.由于AM∥x轴,可得∠BAC=∠AFx=60°.即可得到kAB=tan60°=$\sqrt{3}$,当直线AB的倾斜角为钝角时,同理可得.
解答 解:设抛物线y2=2px(p>0)的准线为l′:x=-$\frac{p}{2}$.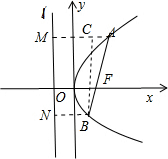
如图所示,
①当直线AB的倾斜角为锐角时,
分别过点A,B作AM⊥l′,BN⊥l′,垂足为M,N.
过点B作BC⊥AM交于点C.
则|AM|=|AF|,|BN|=|BF|.
∵|AF|=3|BF|=$\frac{3}{4}$|AB|,
∴|AM|-|BN|=|AC|=|AF|-|BF|=$\frac{1}{2}$|AB|,
在Rt△ABC中,由|AC|=$\frac{1}{2}$|AB|,可得∠BAC=60°.
∵AM∥x轴,∴∠BAC=∠AFx=60°.
∴kAB=tan60°=$\sqrt{3}$,
直线方程为y=$\sqrt{3}$(x-$\frac{p}{2}$),代入抛物线方程,可得3x2-5px+$\frac{3}{4}$p2=0,
∴|AB|=$\sqrt{1+3}•\sqrt{(\frac{5p}{3})^{2}-{p}^{2}}$=$\frac{8}{3}$p,
②当直线AB的倾斜角为钝角时,可得kAB=-$\sqrt{3}$.|AB|=$\frac{8}{3}$p
综上可知:|AB|=$\frac{8}{3}$p,
故选:D.
点评 本题考查了抛物线的定义及其性质、含60°角的直角三角形的性质、直线的倾斜角与斜率、平行线的性质、分类讨论等基础知识与基本技能方法,属于难题.


科目:高中数学 来源: 题型:选择题
| A. | a>b>c | B. | b>c>a | C. | c>b>a | D. | a>c>b |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8x-6y-7=0 | B. | 3x+4y=0 | C. | 3x+4y-12=0 | D. | 6x+8y-25=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -4 | B. | -3 | C. | 0 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
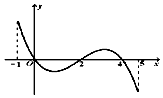 已知函数f(x)的定义域为[-1,5],部分对应值如下表,
已知函数f(x)的定义域为[-1,5],部分对应值如下表,| x | -1 | 0 | 4 | 5 |
| f(x) | -1 | 2 | 2 | -1 |
| A. | ①② | B. | ③④ | C. | ①②④ | D. | ②③④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com