Question

9．已知函数f（x）=2|x+1|-|x-1|
（Ⅰ）求函数f的图象与直线y=1围成的封闭图形的面积m
（Ⅱ）在（Ⅰ）的条件下，若正数a、b满足a+2b=abm，求a+2b的最小值．

Answer 1

分析 （1）首先将函数的解析式写成分段函数的形式，然后绘制函数的图象，结合特殊的坐标即可求得面积值；
（2）利用（1）的结果结合均值不等式的结论求解最值即可．

解答 解：（1）函数$f（x）=2|x+1|-|x-1|=\left\{\begin{array}{l}{-x-3，x≤-1}\\{3x+1，-1＜x＜1}\\{x+3，x≥1}\end{array}\right.$，它的图象如图所示：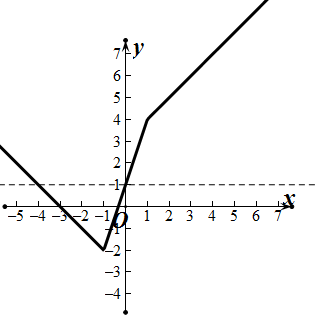



函数f（x）的图象与直线y=1的交点为（-2，1），（0，1），
故函数f（x）的图象和直线y=1围成的封闭图形的面积 $m=\frac{1}{2}×4×3=6$．
（2）由题意可得：a+2b=6ab，则 $\frac{1}{b}+\frac{2}{a}=6$，则：
$（a+2b）（\frac{1}{b}+\frac{2}{a}）=\frac{a}{b}+\frac{4b}{a}+4≥2\sqrt{\frac{a}{b}×\frac{4b}{a}}+4=8$，
当且仅当$a=\frac{2}{3}，b=\frac{1}{3}$ 时等号成立，
则x+2b的最小值是$\frac{8}{6}=\frac{4}{3}$．

点评 本题考查分段函数问题，函数图象的绘制，均值不等式的应用等，重点考查学生对基础概念的理解和计算能力，属于中等题．