
 如图,在梯形ABCD中,AB∥CD,$∠BCD=\frac{2π}{3}$,四边形ACFE为矩形,且CF⊥平面ABCD,AD=CD=BC=CF=1.
如图,在梯形ABCD中,AB∥CD,$∠BCD=\frac{2π}{3}$,四边形ACFE为矩形,且CF⊥平面ABCD,AD=CD=BC=CF=1.分析 (1)在梯形ABCD中,通过AD=CD=BC=1,求出AB=2,通过AB2=AC2+BC2.证明BC⊥AC,证明AC⊥CF,推出AC⊥平面BCF,即可证明EF⊥平面BCF.
(I2)由(I)可建立分别以直线CA,CB,CF为x轴,y轴,z轴的如图所示建立空间直角坐标系,求出平面MAB的一个法向量,求出平面FCB的一个法向量,通过向量的数量积,推出平面MAB与平面FCB所成二面角,然后求解二面角的余弦值.
解答 解:(1)在梯形ABCD中,∵AB∥CD,AD=CD=BC=1,
又∵$∠BCD=\frac{2π}{3}$,∴AB=2,∴AC2=AB2+BC2-2AB•BC•cos60°=3.…(2分)
∴AB2=AC2+BC2.∴BC⊥AC.…(3分)
∵CF⊥平面ABCD,AC?平面ABCD,∴AC⊥CF,…(4分)
而CF∩BC=C,
∴AC⊥平面BCF.…(5分)
∵EF∥AC,∴EF⊥平面BCF.…(6分)
(2)由(1)可建立分别以直线CA,CB,CF为x轴,y轴,z轴的如图所示建立空间直角坐标系,
令FM=λ($0≤λ≤\sqrt{3}$),则C(0,0,0),A($\sqrt{3}$,0,0),B(0,1,0),M(λ,0,1),…(7分)
∴$\overrightarrow{AB}$=(-$\sqrt{3}$,1,0),$\overrightarrow{BM}$=(λ,-1,1),
设$\overrightarrow{n}=(x,y,z)$为平面MAB的一个法向量,
由$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{AB}=0}\\{\overrightarrow{n}•\overrightarrow{BM}=0}\end{array}\right.$得$\left\{\begin{array}{l}-\sqrt{3}x+y=0\\ λx-y+z=0\end{array}\right.$取x=1,则$\overrightarrow{n}$=(1,$\sqrt{3}$,$\sqrt{3}-λ$),…(9分)
∵$\overrightarrow{m}$=(1,0,0)是平面FCB的一个法向量,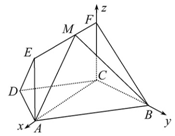
∴$cosθ=\frac{|\overrightarrow{m}•\overrightarrow{n}|}{|\overrightarrow{m}||\overrightarrow{n}|}=\frac{1}{\sqrt{1+3+(\sqrt{3}-λ)^{2}×1}}$=$\frac{1}{\sqrt{(λ-\sqrt{3})^{2}+4}}$.
∵$0≤λ≤\sqrt{3}$,∴当λ=0时,cosθ有最小值$\frac{{\sqrt{7}}}{7}$,…(12分)
∴点M与点F重合时,平面MAB与平面FCB所成二面角最大,此时二面角的余弦值为$\frac{{\sqrt{7}}}{7}$.
点评 本题考查平面向量的数量积的求法,直线与平面垂直的判定定理的应用,考查空间想象能力以及计算能力.


 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案科目:高中数学 来源: 题型:选择题

| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2015 | B. | 2016 | C. | 2017 | D. | 2018 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 18 | B. | 24 | C. | 36 | D. | 48 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,直棱柱ABCD-A1B1C1D1,底面ABCD是平行四边形,AA1=AB=B1D1=3,BC=2,E是边B1C1的中点,F是边CC1上的动点,
如图所示,直棱柱ABCD-A1B1C1D1,底面ABCD是平行四边形,AA1=AB=B1D1=3,BC=2,E是边B1C1的中点,F是边CC1上的动点,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在如图所示的几何体中,四边形ABCD为矩形,平面ABEF⊥平面ABCD,EF∥AB,∠BAF=90°,AD=2,AB=AF=2EF=1,点P在棱DF上.
在如图所示的几何体中,四边形ABCD为矩形,平面ABEF⊥平面ABCD,EF∥AB,∠BAF=90°,AD=2,AB=AF=2EF=1,点P在棱DF上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com