
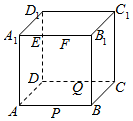
 如图,正方体ABCD-A1B1C1D1的棱长为4,动点E,F在棱A1B1上,动点P,Q分别在棱AB,CD上,若EF=2,现有以下五种说法:
如图,正方体ABCD-A1B1C1D1的棱长为4,动点E,F在棱A1B1上,动点P,Q分别在棱AB,CD上,若EF=2,现有以下五种说法:分析 由长方体的结构特征可知△EFP的面积为定值,Q到平面ABB1A1的距离为定值4,计算出四面体的体积和正方体的体积进行判断.
解答 解:∵CD∥平面EFP,∴Q到平面EFP的距离等于D到平面EFP的距离AD=4.
而S△EFP=$\frac{1}{2}EF×A{A}_{1}$=$\frac{1}{2}×2×4$=4.
∴VQ-EFP=$\frac{1}{3}{S}_{△EFP}•AD$=$\frac{1}{3}×4×4$=$\frac{16}{3}$.
∵正方体体积V正方体=43=64,∴VQ-EFP=$\frac{1}{12}$V正方体.
故①正确,③错误,④正确.
∵CD∥A1B1,∴Q到直线A1B1的距离h为定值,而EF为定值,故△EFQ的面积为定值,故②正确.
又∵四面体PEFQ的体积为定值,∴点P到平面EFQ的距离为定值,故⑤错误.
故答案为:①②④.
点评 本题考查了长方体的结构特征,棱锥的体积计算,属于基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | |$\overrightarrow{a}$-$\overrightarrow{b}$|=1 | B. | ($\overrightarrow{a}$-$\overrightarrow{b}$)⊥$\overrightarrow{b}$ | C. | ($\overrightarrow{a}$-$\overrightarrow{b}$)•($\overrightarrow{a}$+$\overrightarrow{b}$)=$\frac{5}{2}$ | D. | ($\overrightarrow{a}$-$\overrightarrow{b}$)•$\overrightarrow{b}$=-2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [1,+∞) | B. | $[\frac{17}{7},+∞)$ | C. | $[1,\frac{17}{7}]$ | D. | $(-∞,\frac{17}{7}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | -$\frac{3}{4}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com