练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    17．如图中的程序框图表示求三个实数a，b，c中最大数的算法，那么在空白的判断框中，应该填入（　　）
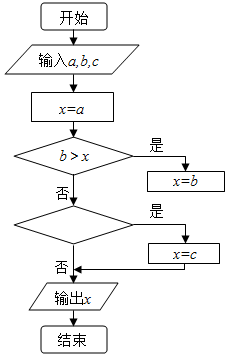
    A．a＞xB．b＞xC．c＜xD．c＞x

    分析 由于该程序的作用输出a、b、c中的最大数，因此在程序中要比较数与数的大小，第一个判断框是判断最大值x与b的大小，故第二个判断框一定是判断最大值x与c的大小．

    解答 解：由流程图可知a、b、c中的最大数用变量x表示并输出，
    第一个判断框是判断x与b的大小，
    则第二个判断框一定是判断最大值x与c的大小，并将最大数赋给变量x，
    故第二个判断框应填入：c＞x．
    故选：D．

    点评 本题主要考查了选择结构的程序框图的应用，算法是新课程中的新增加的内容，也必然是新高考中的一个热点，应高度重视，程序填空也是重要的考试题型，这种题考试的重点有：①分支的条件②循环的条件③变量的赋值④变量的输出，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    8．等比数列{an}的前n项和Sn=2n-1，则${a}_{1}^{2}$+${a}_{2}^{2}$+${a}_{3}^{2}$+…+${a}_{n}^{2}$=$\frac{1}{3}（{4}^{n}-1）$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

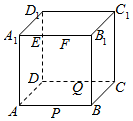    8．如图，正方体ABCD-A1B1C1D1的棱长为4，动点E，F在棱A1B1上，动点P，Q分别在棱AB，CD上，若EF=2，现有以下五种说法：
    ①四面体PEFQ的体积与P，Q点的位置无关
    ②△EFQ的面积为定值
    ③四面体PEFQ的体积与点P的位置有关，与点Q的位置无关
    ④四面体PEFQ的体积为正方体体积的$\frac{1}{12}$
    ⑤点P到平面EFQ的距离随着P的变化而变化
    其中正确的序号是①②④．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    5．对任意实数a，b，c，d，命题：
    ①若a＞b，c≠0，则ac＞bc；
    ②若a＞b，则ac2＞bc2；
    ③若ac2＞bc2，则a＞b．
    其中真命题的个数是（　　）
    A．0B．1C．2D．3

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    12．求点A（0，2）与双曲线x2-y2=1上点的最小距离．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    2．已知i是虚数单位，复数z满足$\frac{1+2i}{z}$=i，则z在复平面上对应的点位于（　　）
    A．第一象限B．第二象限C．第三象限D．第四象限

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．已知等比数列{an}的前n项和为Sn，若S2=6，S4=30，则S6=（　　）
    A．115B．116C．125D．126

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．设点A在-150°角的终边上，|$\overrightarrow{OA}$|=2$\sqrt{2}$（O是坐标原点），则向量$\overrightarrow{OA}$的坐标为（　　）
    A．（$\sqrt{6}$，$\sqrt{2}$）B．（$\sqrt{2}$，$\sqrt{6}$）C．（-$\sqrt{2}$，-$\sqrt{6}$）D．（-$\sqrt{6}$，-$\sqrt{2}$）

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    7．定义：曲线C上的点到直线l的距离的最小值称为曲线C到直线l的距离，已知双曲线C1：$\frac{{y}^{2}}{a}$-x2=1到直线l：y+$\sqrt{2}$=0的距离等于圆C2：x2+y2-8x-10y+16=0到直线l：y+$\sqrt{2}$=0，则实数a=1．

    查看答案和解析>>

    同步练习册答案