
分析 (I)令f(b)-(2b-1)b+b2=1即可解出a;
(II)求出φ′(x),令φ′(x)=0,讨论b的符号得出两根与区间(0,1)的关系,从而得出φ(x)的单调性,得出极值的情形.
解答 解:(I)∵f(x)-(2b-1)x+b2<1的解集为(b,b+1),
即x2+(a-2b+1)x+b2+b<0的解集为(b,b+1),
∴方程x2+(a-2b+1)x+b2+b=0的解为x1=b,x2=b+1,
∴b+(b+1)=-(a-2b+1),解得a=-2.
(II)φ(x)得定义域为(1,+∞).
由(I)知f(x)=x2-2x+b+1,∴g(x)=$\frac{{x}^{2}-2x+b+1}{x-1}$=x-1+$\frac{b}{x-1}$,
∴φ′(x)=1-$\frac{b}{(x-1)^{2}}$-$\frac{k}{x-1}$=$\frac{{x}^{2}-(2+k)x+k-b+1}{(x-1)^{2}}$,
∵函数φ(x)存在极值点,∴φ′(x)=0有解,
∴方程x2-(2+k)x+k-b+1=0有两个不同的实数根,且在(1,+∞)上至少有一根,
∴△=(2+k)2-4(k-b+1)=k2+4b>0.
解方程x2-(2+k)x+k-b+1=0得x1=$\frac{k+2-\sqrt{{k}^{2}+4b}}{2}$,x2=$\frac{k+2+\sqrt{{k}^{2}+4b}}{2}$
(1)当b>0时,x1<1,x2>1,
∴当x∈(1,$\frac{k+2+\sqrt{{k}^{2}+4b}}{2}$)时,φ′(x)<0,当x∈($\frac{k+2+\sqrt{{k}^{2}+4b}}{2}$,+∞)时,φ′(x)>0,
∴φ(x)在(1,$\frac{k+2+\sqrt{{k}^{2}+4b}}{2}$)上单调递减,在($\frac{k+2+\sqrt{{k}^{2}+4b}}{2}$,+∞)上单调递增,
∴φ(x)极小值点为$\frac{k+2+\sqrt{{k}^{2}+4b}}{2}$.
(2)当b<0时,由△=k2+4b>0得k<-2$\sqrt{-b}$,或k>2$\sqrt{-b}$,
若k<-2$\sqrt{-b}$,则x1<1,x2<1,
∴当x>1时,φ′(x)>0,∴φ(x)在(1,+∞)上单调递增,不符合题意;
若k>2$\sqrt{-b}$,则x${\;}_{{1}_{\;}}$>1,x2>1,
∴φ(x)在(1,$\frac{k+2-\sqrt{{k}^{2}+4b}}{2}$)上单调递增,在($\frac{k+2-\sqrt{{k}^{2}+4b}}{2}$,$\frac{k+2+\sqrt{{k}^{2}+4b}}{2}$)上单调递减,在($\frac{k+2+\sqrt{{k}^{2}+4b}}{2}$,+∞)单调递增,
∴φ(x)的极大值点为$\frac{k+2-\sqrt{{k}^{2}+4b}}{2}$,极小值点为$\frac{k+2+\sqrt{{k}^{2}+4b}}{2}$.
综上,当b>0时,k取任意实数,函数φ(x)极小值点为$\frac{k+2+\sqrt{{k}^{2}+4b}}{2}$;
当b<0时,k>2$\sqrt{-b}$,函数φ(x)极小值点为$\frac{k+2+\sqrt{{k}^{2}+4b}}{2}$,极大值点为$\frac{k+2-\sqrt{{k}^{2}+4b}}{2}$.
点评 本小题主要考查二次函数的性质、一元二次不等式与一元二次方程的关系,分类讨论思想,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{5}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{3}{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
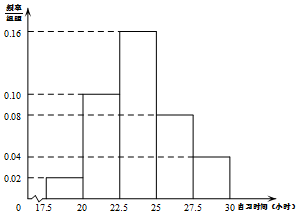 某高校调查了200名学生每周的自习时间(单位:小时),制成了如图所示的频率分布直方图,其中自习时间的范围是[17.5,30],样本数据分组为[17.5,20),[20,22.5),[22.5,25),[25,27.5),[27.5,30].根据直方图,若这200名学生中每周的自习时间不超过m小时的人数为164,则m的值约为( )
某高校调查了200名学生每周的自习时间(单位:小时),制成了如图所示的频率分布直方图,其中自习时间的范围是[17.5,30],样本数据分组为[17.5,20),[20,22.5),[22.5,25),[25,27.5),[27.5,30].根据直方图,若这200名学生中每周的自习时间不超过m小时的人数为164,则m的值约为( )| A. | 26.25 | B. | 26.5 | C. | 26.75 | D. | 27 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com