
分析 设经过点P的椭圆的切线方程为:y-y0=k(x-x0),把y=y0+kx-kx0,代入椭圆方程可得:b2x2+a2$(kx+{y}_{0}-k{x}_{0})^{2}$=a2b2,展开可得△=0,化为:$({a}^{2}-{x}_{0}^{2}){k}^{2}$+2x0y0k+${b}^{2}-{y}_{0}^{2}$=0,把k=$\frac{y-{y}_{0}}{x-{x}_{0}}$(x≠x0)代入上式化简整理即可得出.
解答 证明:设经过点P的椭圆的切线方程为:y-y0=k(x-x0),
把y=y0+kx-kx0,代入椭圆方程可得:b2x2+a2$(kx+{y}_{0}-k{x}_{0})^{2}$=a2b2,
展开为:(b2+a2k2)x2+2a2k(y0-kx0)x+${a}^{2}({y}_{0}-k{x}_{0})^{2}$-a2b2=0,
∵直线与椭圆相切,∴△=$4{a}^{4}{k}^{2}({y}_{0}-k{x}_{0})^{2}$-4(b2+a2k2)[${a}^{2}({y}_{0}-k{x}_{0})^{2}$-a2b2]=0,
化为:$({a}^{2}-{x}_{0}^{2}){k}^{2}$+2x0y0k+${b}^{2}-{y}_{0}^{2}$=0,
把k=$\frac{y-{y}_{0}}{x-{x}_{0}}$(x≠x0)代入上式可得:化为:$({a}^{2}-{x}_{0}^{2})$×$(\frac{y-{y}_{0}}{x-{x}_{0}})^{2}$+2x0y0×$\frac{y-{y}_{0}}{x-{x}_{0}}$+${b}^{2}-{y}_{0}^{2}$=0,
化简整理即可得:方程($\frac{{x}_{0}^{2}}{{a}^{2}}$+$\frac{{y}_{0}^{2}}{{b}^{2}}$-1)($\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$-1)=($\frac{{x}_{0}x}{{a}^{2}}$+$\frac{{y}_{0}y}{{b}^{2}}$-1)2表示过点P的椭圆的两条切线.
点评 本题考查了直线与椭圆相切的性质、一元二次方程的实数根与判别式的关系,考查了推理能力与计算能力,属于难题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在三棱锥P-ABC中,△PAB和△CAB都是以AB为斜边的等腰直角三角形.
如图,在三棱锥P-ABC中,△PAB和△CAB都是以AB为斜边的等腰直角三角形.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
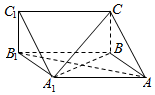 如图,在三棱柱ABC-A1B1C1中,A1A=AB,CB⊥A1ABB1.
如图,在三棱柱ABC-A1B1C1中,A1A=AB,CB⊥A1ABB1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
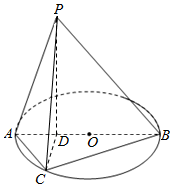 如图所示,已知AB为圆O的直径,点D为线段AB上一点,且AD=$\frac{1}{3}$DB,点C为圆O上一点,且BC=$\sqrt{3}$AC.点P在圆O所在平面上的正投影为点D,PD=DB.
如图所示,已知AB为圆O的直径,点D为线段AB上一点,且AD=$\frac{1}{3}$DB,点C为圆O上一点,且BC=$\sqrt{3}$AC.点P在圆O所在平面上的正投影为点D,PD=DB.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com